케플러의 제2법칙은 "면적속도 일정의 법칙"이라고도 불리며 다음과 같음.
The line from the Sun to any planet sweeps out equal areas of space in equal time intervals.
즉 다음과 같이 태양을 돌고 있는 행성의 타원궤도를 과장해서 그릴 경우,
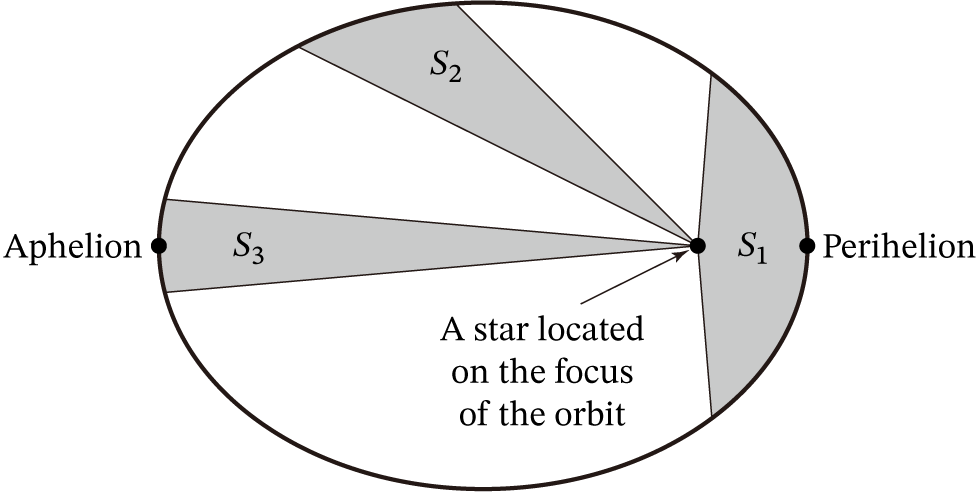
타원궤도를 돌고 있는 행성과 태양을 연결한 선이 같은 시간당 지나간 면적에 대해 $S_1=S_2=S_3$이 성립함.
이를 면적속도 $\frac{dS}{dt}$로 정리하면 다음과 같음
$$\frac{dS}{dt}=\frac{1}{2}r^2\frac{d\theta}{dt}=\frac{1}{2}r (r\omega)$$
좌변이 케플러의 2법칙에 의해 일정하고, $r$이 태양과 행성의 거리이며, $\omega=\frac{d\theta}{dt}$로 각속도임. 행성의 tangential speed $v=r\omega$이므로, 즉 거리와 행성의 tangential speed의 곱이 일정함을 알 수 있음.
행성은 태양의 중력때문에 낙하운동을 하고 있으며 에너지 보존에 따라 다음이 성립함.
태양에 가까워질 경우 위치에너지가 감소하여 운동에너지가 증가하여 속력이 빨라짐.
태양에 멀어질 경우 위치에너지가 증가하고 때문에 운동에너지는 감소하게 되어 속력이 느려짐.
지표에서 위로 던진 돌이 Free fall인 경우, 돌의 높이가 높을수록 위치에너지는 커지고 운동에너지는 감소하여 속력이 느리고, 돌의 높이가 낮을수록 위치에너지는 작고 운동에너지가 커져 속력이 커짐. 태양의 궤도를 도는 행성 역시 태양을 향해 free fall (계속해서 떨어지고 있는 중임)을 하고 있는 것이라고 볼 수 있으며, 역학적 에너지가 보존되고 있다고 생각할 수 있음.
만약 원운동을 하고 있다면, 태양의 중력은 운동방향에 항상 수직으로 가해져 운동의 방향만을 바꾸고 속력은 변화가 없겠지만, 타원운동이기 때문에 태양의 중력의 일부성분이 운동방향에 작용(vector의 분해)하여 속력이 바뀌게 된다. 행성의 운동방향에 평행한 태양의 중력의 일부 성분은 운동에너지를 변화시키게 된다.

'... > Physics' 카테고리의 다른 글
| [Physics] 제2우주속도 & 제3우주속도 (Escape speed) (0) | 2022.05.16 |
|---|---|
| [Physics] 제1우주속도 (0) | 2022.05.16 |
| [Physics] Kepler 3rd Law (케플러의 제3법칙) (1) | 2022.05.16 |
| 원격작용 (Action at a distance) (0) | 2022.05.16 |
| [Physics] Field에 대한 참고자료. (1) | 2022.05.16 |