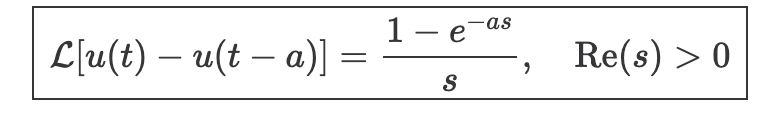
증명1
- 보통 $a>0$ 가정
$$x(t)=u(t)-u(t-a)=
\begin{cases}
1,& 0\le t<a \\
0,& \text{그 외}
\end{cases}$$
이와 같으므로 unilateral transform 은
$$\mathcal{L}[x(t)]
= \int_{0}^{\infty} e^{-st}\big[u(t)-u(t-a)\big] dt
= \int_{0}^{a} e^{-st} dt$$
구간 외에는 0 임.
$\operatorname{Re}(s)>0$에서
$$\int_{0}^{a} e^{-st} dt
= \left[\frac{e^{-st}}{-s}\right]_{0}^{a}
= \frac{1-e^{-as}}{s}.$$
위에 의해 다음이 성립
$$\boxed{\;\mathcal{L}[u(t)-u(t-a)]=\dfrac{1-e^{-as}}{s},\quad \operatorname{Re}(s)>0\;}$$
증명2
Linearity 를 이용해도 증명 가능.
$$\mathcal{L}[u(t)]=\frac{1}{s} \\
\mathcal{L}[u(t-a)]=\int_{a}^{\infty} e^{-st}\,dt=\frac{e^{-as}}{s} \ \ (\operatorname{Re}(s)>0).$$
따라서
$$\mathcal{L}[u(t)-u(t-a)]=\frac{1}{s}-\frac{e^{-as}}{s}=\frac{1-e^{-as}}{s}.$$
같이보면 좋은 자료
2022.10.24 - [.../Signals and Systems] - [SS] Laplace Transform Table
[SS] Laplace Transform Table
SignalLaplace TransformRoC...1$u(t)$$\frac{1}{s}$$\text{Re}(s)>0$ 2$u(t)-u(t-a)$$\frac{1-e^{-as}}{s}$$\text{Re}(s)>0$ 3$\delta(t)$1all complex plane 4$\delta(t-a)$$e^{-as}$all complex plane 5$e^{-at}u(t)$$\frac{1}{s+a}$$\text{Re}(s)>-a$참고6$\cos\Omega_0
dsaint31.tistory.com
'... > Signals and Systems' 카테고리의 다른 글
| Shifted Impulse $\delta(t-a)$의 Laplace Transform (0) | 2025.12.03 |
|---|---|
| From Laplace Transform To z-Transform (0) | 2025.12.03 |
| [SS] 상수 함수에 대한 Unilateral Laplace Transform (0) | 2025.10.30 |
| Lorentzian Function (or Cauchy distribution function) (0) | 2025.10.24 |
| Parseval's Theorem (0) | 2025.10.15 |