Kernel Function이란:
고차원으로의 매핑을 명시적으로 하지 않고도,
그 공간에서의 내적 값(innder product)을 직접 계산할 수 있게 해주는 함수
Kernel Function은
- 머신러닝, 특히 SVM(Support Vector Machine) 과 같은 알고리즘에서 중요한 역할을 하는 함수로
- Similarity를 측정하거나
- 데이터를 고차원 특성 공간으로 매핑하여 비선형 문제를 선형적으로 처리할 수 있는 과정에 핵심적인 역할을 수행함.
1. 수학적 정의:
- Kernel function $K(\textbf{x}, \textbf{y})$는
- 두 데이터 포인트 $\textbf{x}$와 $\textbf{y}$ 사이의 similarity을 측정하는 function.
- 이는 고차원 특성 공간에서의 내적(inner product)을 계산하는 것과 동등함.
- 즉, Kernel function $K(\textbf{x}, \textbf{y}) = \langle \phi(\textbf{x}), \phi(\textbf{y}) \rangle$이며,
- 여기서 $\phi( )$는 원래의 벡터를 고차원 특성 공간으로 매핑하는 함수임.
- $\langle \textbf{x}, \textbf{y} \rangle$ 은 inner prodcut임.
inner product (=dot product)는 두 vector간의 similarity를 측정하는 데에 많이 사용됨:
2. 기능적 정의:
Kernel function은
- 저차원 입력 공간의 데이터를
- 암시적으로 고차원 특성 공간(무한차원의 Reproduction Kernel Hilbert Space)으로 mapping(매핑)하여,
- 비선형 관계를 선형으로 변환하는 역할을 수행.
좀 더 정확하게는 매핑하고 나서의 inner product의 값을 구하는 역할임.
여러 ML 알고리즘이
- Kernel function을 활용하여
- 구하기 어려운 고차원 공간으로의 매핑 후 계산(inner product)을 원래의 공간에서 효율적으로 처리함.
3. 응용 관점:
머신러닝 알고리즘에서 Kernel function은
- 데이터 간의 similarity을 계산하거나,
- 비선형 문제를 선형 알고리즘으로 해결하는 데 사용됨
특히 SVM(Support Vector Machine), PCA(Principal Component Analysis) 등의 알고리즘에서 중요하게 활용됨.
3-1. Kernel Trick과 Kernel Function
Kernel function의 핵심 응용은
'커널 트릭(Kernel Trick)'으로,
이를 통해 실제로 고차원 변환을 수행하지 않고도
고차원 공간에서의 inner product 결과를 얻을 수 있음.
Kernel Trick의 관점으로 본다면, Kernel Function은
- 입력 벡터 $\textbf{a}$, $\textbf{b}$에 기반하여
- “다차원 매핑 변환 $\phi$를 한 후의
dot product$\phi(\textbf{a})^\top \phi(\textbf{b})$”를 - 실제로 매핑변환을 하지 않고도 계산할 수 있는 함수를 가르킴.
Kernel Trick은 Kernel Function으로 매핑 이후의 inner product 계산함:
$$
K(\textbf{x}, \textbf{y}) = \langle \phi (\textbf{x}), \phi(\textbf{y}) \rangle
$$
where,
- $\phi( )$ 는 원래 공간에서 고차원 특성 공간으로의 mapping function.
- Kernel SVM에서 이용하는 특성.
3-2. Kernel Trick 예제
이 예제는 $K(\textbf{a},\textbf{b})=\left(\textbf{a}^\top\textbf{b}\right)^2$ 커널함수(2차 다항식 커널)을 사용한 Kernel Trick임.
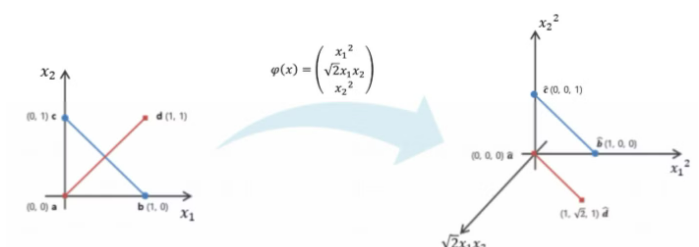
2차 다항식 매핑 $\phi(\textbf{x})$ 에 대해 kernel trick은 다음과 같음:
$$\begin{aligned}\phi(\textbf{a})^\top \phi(\textbf{b}) &= \left(\begin{matrix} a_1^2 \\\sqrt{2}a_1a_2 \\ a^2_2\end{matrix}\right)\cdot \left(\begin{matrix} b_1^2 \\ \sqrt{2}b_1 b_2 \\b_2^2 \end{matrix} \right) \\ &= a_1^2b_1^2+2a_1b_1a_2b_2+a_2^2b_2^2 \\ &=\left(a_1b_1+a_2b_2 \right)^2\\ &= \left(\left(\begin{matrix}a_1 \\a_2 \end{matrix}\right)^\top \left( \begin{matrix} b_1 \\ b_2 \end{matrix}\right)\right)^2\\&=\left(\textbf{a}^\top\textbf{b}\right)^2\end{aligned}$$
$$\therefore \phi(\textbf{a})^\top\phi(\textbf{b})=\left(\textbf{a}^\top\textbf{b}\right)^2$$
- 즉, 훈련데이터 들을 직접적으로 2차 다항식 함수로 변환한 것이 아닌, inner product 후 해당 2차 다항식 함수를 적용하는 Kernel function으로 동일한 결과를 얻음.
- Kernel function을 이용할 경우, 계산량 등에서 매우 효율적임.
- 위의 예제에서, kernel 사용시 내적을 위한 곱셈 2번과 변환을 위한 곱셈 1번으로 끝남!
- 여기서 Kernel 함수 는 일반적으로 입력 벡터 $\textbf{a}$, $\textbf{b}$에 기반하여 다차원 매핑 변환 $\phi$를 한 후의
dot product$\phi(\textbf{a})^\top \phi(\textbf{b})$를 계산할 수 있는 함수를 가르킴.
4. 다른 분야의 Kernel과의 비교
- 선형대수학의 Kernel:
- 정의: 선형 변환의 null space (영공간)를 의미.
- 특징: $A\textbf{x} = \textbf{0}$을 만족하는 벡터 $\textbf{x}$의 집합.
- 차이점: 머신러닝의 kernel function과는 달리, linear transform의 특성을 나타내는 개념.
- 컨볼루션(Convolution)의 Kernel:
- 정의: 입력 데이터에 적용되는 filter 또는 mask (or impulse response)를 의미.
- 특징: 이미지 처리나 신호 처리에서 주로 사용되며, 특정 특징을 추출하거나 변환하는 데 활용됨.
- 유사점: 머신러닝의 kernel function과 마찬가지로 데이터 변환에 사용되지만, 적용 방식과 목적이 다름.
- 확률에서의 Kernel (KDE):
- 정의: 확률 밀도 함수를 추정하는 데 사용되는 가중치 함수.
- 특징: Kernel Density Estimation(KDE)에서 데이터 포인트의 분포를 부드럽게 추정하는 데 사용됨.
- GMM과의 관계: KDE는 비모수적 방법이며, GMM(Gaussian Mixture Model)은 모수적 방법임. KDE는 각 데이터 포인트에 커널 함수를 적용하고, GMM은 여러 가우시안 분포의 혼합으로 밀도를 추정함.
- 유사점: 머신러닝의 kernel function처럼 데이터의 특성을 변환하는 역할을 하지만, 목적과 적용 방식이 다름.
- 운영체제(OS)에서의 Kernel:
- 정의: 운영체제의 핵심 부분으로, 하드웨어와 소프트웨어 사이의 중개자 역할을 함.
- 특징: 메모리 관리, 프로세스 관리, 장치 드라이버 관리 등 핵심적인 시스템 기능을 수행함.
- 차이점: 머신러닝의 kernel function과는 완전히 다른 개념으로, 시스템 소프트웨어의 일부를 지칭함.
참고: Kernel의 어원
Kernel이라는 용어는 라틴어 'corneum'에서 유래했으며, '씨앗의 핵' 또는 '중심'을 의미함.
이 개념이 다양한 분야에 적용되면서 각 분야에서 '핵심' 또는 '중요한 부분'을 나타내는 데 사용됨.
머신러닝에서 Kernel function은 데이터 분석의 '핵심' 역할을 하는 함수라는 의미에서 이 이름이 붙은 것으로 알려짐. 이 함수가 데이터 변환과 유사성 측정의 중심에 있기 때문임.
5. 조금 더 엄밀(?)한 수학적 정의
Kernel SVM에서 사용되는 Kernel function은 아래의 정의를 만족해야한다.
- 대칭성 (symmetry)
- $K(x_1,x_2) = K(x_2,x_1)$
- SVM등에 이용될 경우, $K(x_1, x_2)=K(x_2, x_1)$
- Positive Semidefiniteness
- Kernel함수로부터 정의 된 Gram Matrix는 Positive Semi-definiteness 를 만족해야함.
- 즉, 임의의 벡터 집합 ${\textbf{x}_1, \textbf{x}_2, \dots, \textbf{x}_n }$에 대해, Gram Matrix $G$가 positive semidefinite (양의 준정부호)임.
- Gram Matrix $G$의 원소 $G_{i,j} = K(\textbf{x}_i, \textbf{x}_j)$ 임.
- Kernel함수로부터 정의 된 Gram Matrix는 Positive Semi-definiteness 를 만족해야함.
5-1. Mercer’s Theorem
위의 조건들을 만족하는 function은 Mercer’s Theorem에 의해 Kernel Function으로 사용가능함.
Mercer's Theorem은
- 주어진 커널 함수가
- 재생 커널 힐베르트 공간(Reproducing Kernel Hilbert Space, RKHS)의 내적(inner product)으로
- 표현될 수 있는지를 판별하는 중요한 도구
Mercer's Theorem은
- 특정 커널 함수가 양의 준정부호성과 대칭성을 만족할 때,
- 해당 커널 함수는 데이터 공간을 더 높은 차원으로 매핑하는 함수로 사용할 수 있음을 의미
5-2. 재생성 커널 힐베르트 공간 (RKHS):
- 모든 유효한 Kernel function은
- Reproducing Kernel Hilbert Space(RKHS, 재생성 커널 힐베르트 공간)과 연관됨.
- RKHS 에서 Kernel Function은 inner product를 reproducing하는 역할을 함.
6. 대표적 kernel functions
다음의 function들이 scikit-learn의 SVC 클래스에서 주로 이용되는 kernel function임: kernel 인수를 지정하여 커널을 설정할 수 있음.
- Linear function (
linear) : $K(\textbf{a},\textbf{b})=\textbf{a}^\top\textbf{b}$ - Polynomial function (
poly) : $K(\textbf{a},\textbf{b})=\left( \gamma \textbf{a}^\top\textbf{b} +r \right)^d$gamma: $\gamma$coef0: $r$degree: $d$
- Gaussian Radial Basis Function (
rbf) : $K(\textbf{a},\textbf{b})=\exp \left( -\gamma | \textbf{a} - \textbf{b} |^2_2 \right)$gamma: $\gamma$
- Sigmoid (
sigmoid) : $K(\textbf{a},\textbf{b})=\tanh \left( \gamma \textbf{a}^\top\textbf{b} +r \right)$gamma: $\gamma$coef0: $r$
2024.09.26 - [Programming/ML] - [ML] Radial Basis Function Kernel (RBF Kernel)
[ML] Radial Basis Function Kernel (RBF Kernel)
RBF KernelRBF 커널 또는 Gaussian 커널이라고도 불리는 함수머신 러닝에서 Kernel Function으로 널리 사용되는 함수서포트 벡터 머신(SVM), 커널 PCA 등의 알고리즘에서 사용.similarity 계산 및 고차원 feature sp
dsaint31.tistory.com
'Programming > ML' 카테고리의 다른 글
| [ML] Embedding: (2) | 2024.09.28 |
|---|---|
| [ML] Embedding의 수학적 정의 및 Embedding Layer (0) | 2024.09.28 |
| [ML] Radial Basis Function Kernel (RBF Kernel) (1) | 2024.09.26 |
| [ML] Ensemble 기법 (0) | 2024.09.08 |
| [ML] Constrained Least Squares: Lagrangian 을 활용. (1) | 2024.07.16 |