요약
optimization에서 Duality 는 primal problem과 dual problem의 관계를 의미함.
이를 이용하여,
- 원래 최적화(minimization ro maximization)해야 할 문제인 primal problem을 직접 푸는 대신에,
- duality를 이용하여 이에 해당하는 dual problem을 구하고,
- 참고로, primal L(x,λ,ν)가 L:Rn×Rm×Rp→R 인 반면,
- dual D(λ,ν)은 D:Rm×Rp→R임.
- 해당 dual problem이 보다 쉽게 풀리는 경우,
- 이를 풀어서optimal solution 및 optimal value를 구할 수 있다.
Duality 는
- Weak Duality 관계와
- Strong Duality 관계,
두가지 경우로 나뉘며,
각각의 경우에 따라 dual program을 활용하는 방식이 조금 차이가 있다.
Weak duality relationship의 dual problem을 사용할 경우,
- primal solution을 직접 구하는 대신
- primal solution의 lower boundary를 제공하는 dual problem을 풀어서
- optimal solution이 존재할 수 있는 feasible region을 줄이고
- 그 줄어든 feasible region에서 evalution 등을 통해 optimal solution과 optimal value를 구한다.
Strong duality relationship의 dual problem을 사용할 경우,
- dual problem의 optimal solution과 optimal value가
- primal problem의 경우와 일치하기 때문에
- dual problem의 optimization을 통해 직접적으로 primal problem을 구할 수 있다.
단, Strong duality 관계가 항상 성립하는 것은 아니다.
실제로 Duality와 관련된 여러 조건들 (Slater's condition, Mangasarian-Fromovitz condition (MFC or Mangasarian-Fromovitz constraint qualification (MFCQ)), KKT conditions 등)이 있으며, 이들 condition들을 통해 duality가 strong인지 여부를 확인하거나 optimal solution의 범위를 줄여 optimization을 풀게 된다.
2023.07.06 - [.../Math] - [Math] Slater's Condition
[Math] Slater's Condition
Slater's condition은 Strong Duality의 Sufficient Condition으로 유명하고, 동시에, Slater's condition을 만족하는 경우에는 KKT가 necessary condition이 되기 위해 선행적으로 요구되는 Regularity Condtion이 성립된다는 성
dsaint31.tistory.com
2023.05.17 - [.../Math] - [Math] Karush-Kuhn-Tucker Conditions (KKT Conditions)
[Math] Karush-Kuhn-Tucker Conditions (KKT Conditions)
KKT Conditions KKT조건은 inequality constraints을 가지는 contrained optimization problem의 optimal solution이 만족해야하는 necessary condition들의 집합(4개의 necessary condition)임. Lagransian multiplier를 도입하여 equality const
dsaint31.tistory.com
실제 활용?
개인적으로 dual problem등을 푸는 데에 가장 많이 쓰이는 것이 Karush-Kuhn-Tucker Conditions 이라고 생각되며, Optimization을 공부할 때에나 Slater's condition 이나 MFCQ를 사용해보는 거 같다.
실제로,
- Linear Programming(LP)이나 Quadratic Programming(QP)의 경우
KKT conditins를 통해 dual problem을 풀면
실제 primal problem과 동일한 optimal solution과 optimal value를 구할 수 있다 (즉, Strong Duality). - QP를 제외한 non-linear programmign의 경우,
KKT조건은 necessary condition이기 때문에 optimal solution인지를 evaluation(= Weak Duality관계임.)해야 한다.
엄격하게 애기하면, Regularity Condition 부터 확인해야 한다.
대상 문제가 Regularity Condition을 만족하지 않는 경우에는 KKT conditions이 necessary condition임을 보장할 수 없기 때문에 이것부터 확인해야 하지만, ==;; 대부분 Regularity Condition이 만족하는 경우만 다루는터라...
Duality (=Weak duality)
최적화에서 Weak duality는 다음과 같다.
duality or the duality principle is the principle that
- optimization problems may be viewed from either of two perspectives,
- the primal problem or
- the dual problem.
The solution to the dual problem provides a lower bound to the solution of the primal (minimization) problem.
즉, weak duality 관계에서는
- “primal problem의 feasible solution에서의 object function의 값”이
- 항상 “dual problem 의 feasible solution에서의 object function의 값보다 크거나 같게 된다”(lower bound를 제공)
Mangasarian-Fromovitz condition 을 만족하는 경우 weak duality가 성립.
Object function을 최소화하는 Primal problem이 non convex인 경우에도
Dual problem은 항상 concave maximization problem (구하고자 하는 Lagrangian multipler에 대해)이 성립한다.
때문에 잘 알려진 convex optimization method 들을 적용하기 쉽다는 장점을 가진다.
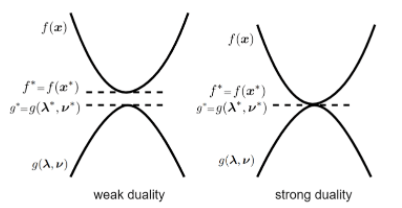
Daulity Gap
앞서 살펴본 Weak Duality에서 언급되었듯이
- dual problem은 lower bound를 제공하기 때문에
- Dual problem의 optimal value가 반드시 Primal problem의 optimal value와 같은 건 아님.
이처럼 같지 않은 경우 이들 간의 차이를 duality gap이라고 함.
(일반적으로 weak duality에서 dulity gap은 0이 아니다. 0인 경우, strong duality라고 부름)

즉, duality gap이 0인 경우 Strong duality를 만족하다고 애기함.
Strong duality에서는 primal과 dual의 각 optimal solution에서의 objective function의 optimal value가 같음.
Strong duality
“Primal problem의 최적해의 object function의 값”과
이의 “dual problem의 최적해의 object function의 값”이 같은 경우를
strong duality관계라고 부름.
strong duality가 성립하는 경우,
- primal problem을 dual problem으로 바꾸어 풀 수 있다 (optimal value와 optimal solution이 같음).
- 다행히도 convex optimization problem의 경우, strong duality관계가 성립한다.
- 참고로, SVM은 convex optimization (=quadratic programming)임
Slater’s condition을 만족하며 strong duality관계가 됨.
엄밀하게 애기하면, Slater's condition은 strong duality의 sufficient condition이다.
즉, Slater's condition을 만족하지 않는다해도 strong duality일 수 있다.
읽어보면 좋은 자료
https://gazelle-and-cs.tistory.com/m/17
[선형 계획법] 쌍대성(Duality)
Linear programming은 최적화 분야에서 잘 알려지고 연구되었으며 실제로도 많이 응용되는 기법입니다. 줄여서 LP라고도 하며, 우리말로는 선형계획법으로 불립니다. 이름이 뭔가 멋들어져서 괜스레
gazelle-and-cs.tistory.com
https://ratsgo.github.io/convex%20optimization/2018/01/25/duality/
Duality · ratsgo's blog
이번 글에서는 Duality와 관련된 개념들을 살펴보도록 하겠습니다. 이 글은 미국 카네기멜런대학 강의를 기본으로 하되 영문 위키피디아 또한 참고하였습니다. 그럼 시작하겠습니다. concept 최적
ratsgo.github.io
https://pasus.tistory.com/91?category=1135399
[KKT 조건 - 3] 프라이멀 문제와 듀얼 문제
최적화 문제는 두 가지 관점에서 문제를 표현할 수 있는데 프라이멀 문제(primal problem)와 듀얼 문제(dual problem)가 그것이다. 어떤 문제에서는 프라이멀 문제보다도 듀얼 문제로 바꾸어 푸는 것이
pasus.tistory.com
'... > Math' 카테고리의 다른 글
| [Math] Linear Programming and Quadratic Programming (0) | 2023.07.08 |
|---|---|
| [Math] A regular point of the feasible set. (0) | 2023.07.07 |
| [Math] Slater's Condition (0) | 2023.07.06 |
| [Math] Lagrangian from Standard Form using Indicator Function (0) | 2023.07.06 |
| [Math] Lagrangian Primal and Lagrangian Dual (0) | 2023.07.05 |