이 문서는 Numerator Layout Convention을 따름.
Jacobian은
vector field (or multi-variate vector-valued function)에 대한
1st order derivative에 해당함.
정의
input과 output이 vector인 vector function(←vector field, $\textbf{f}:\mathbb{R}^n\to\mathbb{R}^m$)을 input vector로 미분!
→ Jacobian matrix ($m \times n$ matrix) : row는 output, column은 input에 해당(column vector사용시)
Take $\textbf{f}: \mathbb{R}^n \rightarrow \mathbb{R}^m$ a function such that its first-order partial derivatives exist on $\mathbb{R}^n$.
It takes a point $\textbf{x} \in \mathbb{R}^n$ as input and produce the vector $\textbf{f}(\textbf{x})\in\mathbb{R}^m$ as output.
Then the Jacobian matrix of $\textbf{f})$ is as follows;
$$J_{\textbf{f}} (\textbf{x})=\begin{bmatrix}\frac{\partial f_1}{\partial x_1} & \frac{\partial f_1}{\partial x_2} &\cdots & \frac{\partial f_1}{\partial x_n} \\ \frac{\partial f_2}{\partial x_1} & \frac{\partial f_2}{\partial x_2} &\cdots & \frac{\partial f_2}{\partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial f_m}{\partial x_1} & \frac{\partial f_m}{\partial x_2} &\cdots & \frac{\partial f_m}{\partial x_n} \end{bmatrix}=\begin{bmatrix}\nabla{f_1}^T \\ \nabla{f_2}^T \\ \vdots \\ \nabla {f_m}^T \end{bmatrix}= \frac{\partial \textbf{f}}{\partial \textbf{x}}$$
- gradient $\nabla f_i(\textbf{x})$ 는 column vector로 정의되기 때문에 numerator layout convetion에서 $\nabla f_i(\textbf{x})=\left[ \frac{\partial f_i}{\partial \textbf{x}}\right]^T$ 이다.
- gradient를 구할 때, $f:\mathbb{R}^n \to \mathbb{R}$이고, numerator layout conventino에서 output의 dimention은 numerator가 기준이므로 derivative of $f$ 는 output이 scalar (=$1\times 1$ matrix)인 $f$를 따라 row-vector ($1\times n$ matirx)로 나오게 된다.
$$\frac{\partial f}{\partial \textbf{x}}= \begin{bmatrix} \frac{\partial f}{\partial x_1} \cdots \frac{\partial f}{\partial x_n}\end{bmatrix} = \langle \frac{\partial f}{\partial x_1}, \cdots, \frac{\partial f}{\partial x_n} \rangle$$.
넋두리
만약, gradient를 row vector로 생각하면 tanspose가 필요없다.
손으로 계산할 때,
numerator layout 으로 할지 denominator laytout으로 할지에 따라
벡터와 행렬의 미분 결과가 다르게 보이게 된다.
때문에, layout을 일관되게 지켜야 하지만 (특히 손으로 계산시),
실제 사용할 때는 대부분의 경우 이미 구현된 library를 쓰기 때문에 개념적인 이해만 남아있게 되고...
이로 인해 표기에서 섞이게 되는 경우가 정말 많다.
사실 연필로 푸는 경우는 학교에서나 하지... 실제로는 --;;;
때문에 표기에서 혼재되는 경우가 많다.
실제 인터넷 상의 문서들을 읽다보면 나같은 사람이 많구나 할 정도로 layout convetion이 혼재된 것을 보게 된다.
그래도 가급적이면 convention을 엄격히 지키려고 노력하는 게 좋다.
다음이 성립함
$$
\textbf{f}(\textbf{x})=\begin{bmatrix} f_1 \\ f_2 \\ \vdots \\ f_m \end{bmatrix} , J_{\textbf{f}(\textbf{x})}\textbf{x}=\begin{bmatrix} \frac{\partial f_1}{\partial x_1} & \frac{\partial f_1}{\partial x_2} &\cdots & \frac{\partial f_1}{\partial x_n} \\ \frac{\partial f_2}{\partial x_1} & \frac{\partial f_2}{\partial x_2} &\cdots & \frac{\partial f_2}{\partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial f_m}{\partial x_1} & \frac{\partial f_m}{\partial x_2} &\cdots & \frac{\partial f_m}{\partial x_n} \end{bmatrix}\begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix}
$$
Example 1
다음 $\textbf{f}(\textbf{x})$의 $\textbf{x}$에 대한 jacobian을 구하시오.
$$
\textbf{f}(\textbf{x})=\begin{bmatrix}
\rho\cos(\phi) \\ \rho\sin(\phi) \\ \rho^2
\end{bmatrix} , \textbf{x}=\begin{bmatrix}
\rho \\ \phi
\end{bmatrix}
$$
from IPython.display import HTML, Math
from sympy import sin, cos, Matrix, latex
from sympy.abc import rho, phi
f = Matrix([rho*cos(phi), rho*sin(phi), rho**2])
display(Math(f'\\textbf f (\\textbf x )={latex(f)}'))
x = Matrix([rho, phi])
display(Math(f'\\textbf x={latex(x)}'))
a = r"J_{\textbf{f}(\textbf{x})}"
b = latex(f.jacobian(x))
display(Math('{}={}'.format(a,b)))결과는 다음과 같음.

1st order drivative : Gradient and Jacobian
1st order differentiation 으로 다음을 기억할 것.
- 1st order derivative of scalar function : (ordinary) derivative
- 1st order derivative of multi-variable function (or scalar field) : gradient
- 1st order derivative of vector-valued multi-variable function (or vector field) : Jacobian
Jacobian이나 gradient 모두 1st order derivative 의 특징을 가지고 있음.
특정 function의
- 지역적인 변화 (e.g. scalar function에서의 기울기)를 파악하거나,
- 해당 지역적인 변화에 대한 linear approximation을 구하거나,
- 또는 함수의 극대, 극소 등을 찾을 때 사용됨 (정확히는 stationary point이고 2계도함수를 통해 확인해야함).
Gradient와 Jacobian
$$
J_{\textbf{f}}=\begin{bmatrix}\nabla{f_1}^T \\ \nabla{f_2}^T \\ \vdots \\ \nabla {f_m}^T \end{bmatrix}=\begin{bmatrix} \frac{\partial f_1}{\partial x_1} & \frac{\partial f_1}{\partial x_2} &\cdots & \frac{\partial f_1}{\partial x_n} \\ \frac{\partial f_2}{\partial x_1} & \frac{\partial f_2}{\partial x_2} &\cdots & \frac{\partial f_2}{\partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial f_m}{\partial x_1} & \frac{\partial f_m}{\partial x_2} &\cdots & \frac{\partial f_m}{\partial x_n} \end{bmatrix}
$$
- scalar field $f(\textbf{x})$를 vector $\textbf{x}$로 1차 미분하면 gradient $\nabla f(\textbf{x})$ (gradient는 vector field임).
- 해당 gradient를 다시 vector $\textbf{x}$로 미분하면 gradient에 대한 Jacobian matrix이며, 이를 $f(\textbf{x})$의 Hessian matrix라고 부름.
$$H[f]=H=\left(J\left[\nabla f\right]\right)^T$$
참고로, Hessian matrix는
- $f$가 이차미분 가능하고 해당 이차미분 결과가 연속일 경우에는
- 항상 symmetric이기 때문에
- 이 경우엔, transpose를 하지 않아도 같은 결과임..
Hessian matrix에 대해 좀 더 자세한 내용은 다음을 참고하라.
https://dsaint31.tistory.com/entry/Math-Hessian-Summary
[Math] Hessian : Summary
이 문서는 Numeartor Layout Convention 을 사용함. Hessian : Summary 2nd order derivative of multivariate functoin. 여기서 multivariate function은 입력은 vector, 출력은 scalar Hessian matrix는 다음과 같음. $$ \begin{aligned}Hf(\textbf
dsaint31.tistory.com
Example 2
$T: \mathbb{R}^2 \rightarrow \mathbb{R}^4$ 인 function $\textbf{f}(x_1,x_2)$이 다음과 같을 경우, Jacobian matrix를 구하라.
$$
\textbf{f}(x_1,x_2)=\left(2x_1+x_2, \sum^2_{i=1}x_i, x_1x_2, x_1^2\right)
$$
import sympy as sp
x_1, x_2 = sp.symbols('x_1 x_2')
x = sp.Matrix([x_1,x_2])
f = sp.Matrix([2*x_1+x_2, x_1+x_2, x_1*x_2, x_1**2])
f.jacobian(x)
기하학적 의미 와 Determinant of Jacobian
Jacobian matrix는 어떤 함수(비선형 함수포함)에 대한, 국소적인 선형변환 근사 (local linear approxiamtion or local linearization)임.
어떤 비선형 함수가 있고, 특정 점 $(x_0,y_0)$에서 이들이 국소적인 변화량은 $dx$, $dy$일 때, 이들을 국소적 선형근사인 $du$,$dv$로 구하는데 Jacobian이 사용된다.
- 주의할 것은, 아래의 $\times$는 곱하기 를 의미함. cross product가 아님.
$$
\begin{bmatrix} dx \\ dy \end{bmatrix} = J \begin{bmatrix}du \\ dv\end{bmatrix} = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} du \\ dv \end{bmatrix}
$$
$$
dx = a\times du + b\times dv \\ dy= c \times du + d \times dv\\ J = \begin{bmatrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \end{bmatrix}= \begin{bmatrix} \frac{\partial f_1}{\partial u} & \frac{\partial f_1}{\partial v} \\ \frac{\partial f_2}{\partial u} & \frac{\partial f_2}{\partial v} \end{bmatrix}
$$
$$dx \times dy = |\text{det }J| (du \times dv)=\left| \text{det} \begin{bmatrix}\frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v}\end{bmatrix}\right|( du \times dv)$$
- 여기서 $du$, $dv$를 x축과 y축의 단위 변화라고 생각하면 아래 그림에서 비선형 변환 $\textbf{f}$ (상단)에 의한 해당 단위 변화가 $dx$, $dy$로 변환됨.
- $(du \times dv) \underset{\textbf{f}}{\to} (dx \times dy)$
- 이 경우, $du$, $dv$가 1씩 변화한 단위면적이 $dx$,$dy$에서는 $|\text{det}J|$의 면적변환으로 바뀜.
- 이때 비선형 변화 $\textbf{f}$를 국소적으로 보면 일종의 선형변환(하단)이라고 볼 수 있으며, 해당 선형변환이 바로 Jacobian임.
- 때문에, Jacobian의 determinant는 $f$에 의한 변환에 따른 단위 면적의 변화에 해당. ($du \times dv$가 변환 전 단위면적으로 1이고, 이 단위면적이 변환 후 $dx \times dy$의 면적으로 바뀌며 그 값이 바로 Jacobian의 determinant임.)
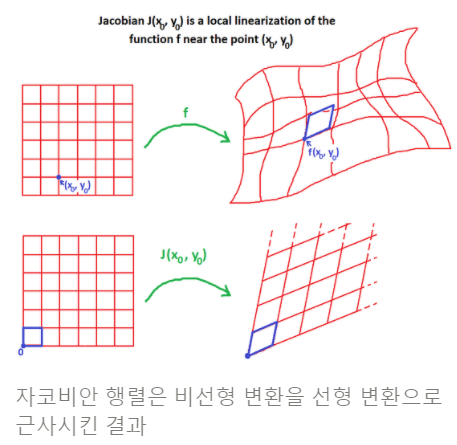
Jacobian의 determinant를 이용한 linear approixmation은 주로 $\textbf{f}:\mathbb{R}^n \to \mathbb{R}^n$ 과 같이 square matrix로 표현되는 경우(domain과 codomain의 차원이 같은 경우)에만 사용된다. (determinant는 square matrix에서만 구할 수 있음)
다음과 같은 좌표계 변환시 단위 면적, 혹은 단위 부피의 변화되는 정도가 바로 Jacobian의 determinant임.
- 2D : cartesian coordinate system에서 polar coordinate system으로 변환
- 3D : cartesian coordinate system에서 Spherical Coordinate System으로 변환
Referenece
Grant Sanderson의 Khan Academy Jacobian 강의
What do I do with these equations to create a Jacobian matrix?
My instructions were to find equilibrium values (the picture I added is only showing E0, I was hoping if I got it figured out I could do the others rather than someone try to do all of them for me),
math.stackexchange.com
'... > Math' 카테고리의 다른 글
| [Math] Kullback-Leibler Divergence (1) | 2022.05.12 |
|---|---|
| [Math] Matrix Calculus : Numerator Layout (0) | 2022.05.08 |
| [Math] Commonly used Vector derivatives. (0) | 2022.05.05 |
| [Statistics] Covariance vs. Correlation: (0) | 2022.05.01 |
| [Statistics] Sample Point Method (0) | 2022.05.01 |