directional derivative

[Math] Gradient (구배, 기울기, 경사, 경도) Vector

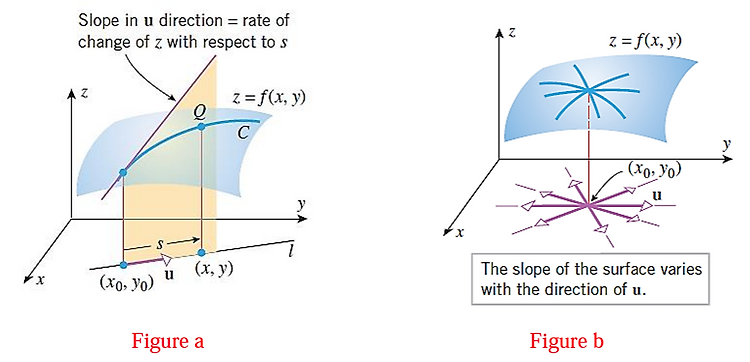
Gradient (구배, 기울기, 경사, 경도), $\nabla f(\textbf{x})$ multivariate function (=scalar field) $f(\textbf{x})$에서 input $\textbf{x}$의 미세한 변화에 대해 output이 1) 가장 가파르게 증가하는 direction(방향)과 2) 그 증가하는 변화율의 정도를 magnitude(크기)로 가지는 vector field (multivariate vector valued function)를 구하는 것이 바로 Gradient $f(\textbf{x})$=$\nabla f(\textbf{x})$임. Gradient를 통해, scalar field $f(\textbf{x})$(← Potential Energy, Voltage,..

[Math] Directional Derivative (방향도함수)

정의 Function $f:\mathbb{R}^n\to \mathbb{R}$에 대해서 unit vector $\textbf{u}=\begin{bmatrix}u_1 & \cdots & u_n\end{bmatrix}^T$의 방향으로 function $f$의 순간변화율이 바로 Directional Derivative임. 수식 $$\nabla_{\textbf{u}}f(\textbf{x})=\underset{h \to 0}{\lim}\frac{f(\textbf{x}+h\textbf{u})-f(\textbf{x})}{h}=\frac{\partial f(\textbf{x})}{\partial \textbf{u}}$$ Directional Derivative에서 방향을 결정하기 위해서 unit vector $\text..