derivative

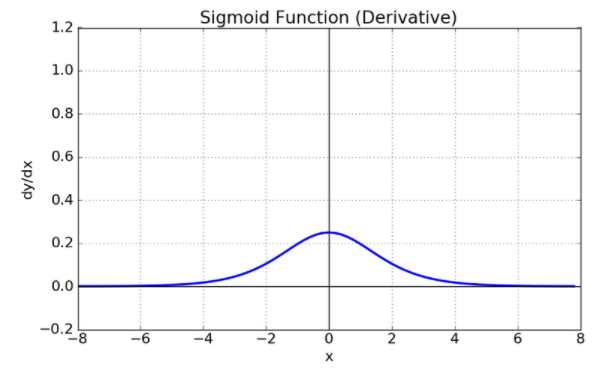
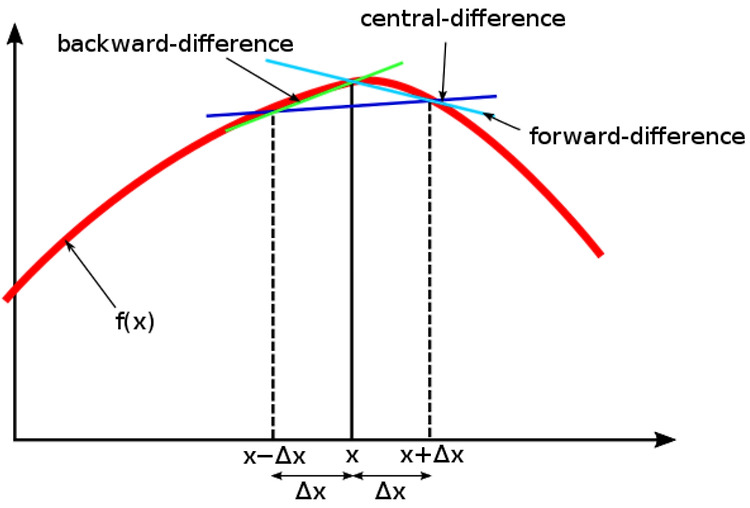
[Math] The Key Rules of Differentiation

The Key Rules of Differentiation 1. Power rule (다항식의 미분에 핵심) If $f(x)=x^n$, where $n \in \mathbb{R}$, then the derivative of $f$ with respect to $x$ is $f^\prime(x)=nx^{n-1}$. 2. Constant rule if $f(x)=c$ where $c \in \mathbb{R}$ and constant, then the derivative of $f$ with respect to $x$ is $f^\prime (x)=0$. 3. Sum and Difference rule (미분의 선형성) $f$와 $g$ 모두 $x$에 대해 differentiable function이라면, 다..

[Math] Derivative of Logistic Function

Derivative (도함수) of Logistic Function (Sigmoid라고도 불림) $y=\sigma(x)=\dfrac{1}{1+e^{-x}}$ 를 미분하면 다음과 같음. $$\frac{d}{dx}\sigma(x)= \sigma(x)(1-\sigma(x))$$ graph 유도 유도는 다음과 같음. $$\begin{aligned}\frac{d}{dx}\sigma(x)&= \dfrac{0\times(1+e^{-1}) - 1\times(-e^{-1})}{(1+e^{-x})^2}\\&=\dfrac{e^{-x}}{(1+e^{-x})^2}\\ &= \frac{1}{(1+e^{-x})}\frac{e^{-x}}{(1+e^{-x})}\\ &= \frac{1}{(1+e^{-x})}\left( 1-\dfrac{..

[Math] Differentiation (or Differential, 미분)과 Difference (차분)

"Differential을 구한다(Differentiation, 미분하다)" 는 derivative(도함수)를 구하는 것을 가르킴. Derivative(도함수)는 average rate of change (평균변화율)의 limit인 instantaneous rate of change (순간변화율←linear approximation의 slope)임. $$ \displaystyle \dfrac{dy}{dx}=y^\prime=\lim_{\Delta x \to 0}\dfrac{f(x+\Delta x)-f(x)}{\Delta x}=\lim_{\Delta x \to 0}\dfrac{\Delta f(x)}{\Delta x} $$ 좀 더 길게 애기한다면, function의 모든 점에서의 순간변화율을 구하는 funct..