Sinusoid

[Physics] A periodic representation of wave : sin and cos

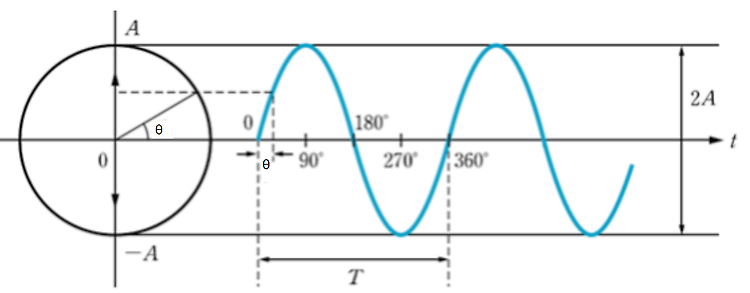
$\sin$(정현), $\cos$(여현) : 주기신호나 wave등을 나타내는데 사용되는 기본적인 함수. $$ y(t)= A \sin(\omega t + \theta) \\ y(t) = A \cos (\omega t + \theta)$$ $T$ : period (주기), 단위 : sec. Time to complete one vibration $\omega$ : Angular frequency (각주파수), 단위 : raidan/sec (보통 기재하지 않음). 오른쪽의 회전운동에서 단위시간(=보통 1sec)당 몇 radian을 움직이는지 를 의미함. $\omega = \dfrac{2\pi}{T} = 2\pi f$ $f$ : frequency (진동수, 주파수), Hz(=1/sec). How frequent..

[SS] FT of phase shifted sinusoid!

$f(t)=A\sin (\omega_0 t-\theta)$ 에 대한 Fourier Transform 구하기. 1. phase가 없는 경우를 구하고 $\mathscr{F}[\sin \omega_0 t]$ 는 다음과 같음. $$\begin{aligned}\mathscr{F}[\sin \omega_0 t] & = \int_{-\infty}^{\infty} \sin \omega_0 t e^{-j\Omega t} dt\\ &= \int_{-\infty}^{\infty} \frac{e^{j\omega_0 t}-e^{-j\omega_0 t}}{2j} e^{-j\Omega t} dt \\ &= \frac{1}{2j} \left\{ \int_{-\infty}^{\infty} e^{j\omega_0 t} e^{-j\Ome..