1. 정리
$N$개의 event (사상,사건)인 $H_0, H_1, ... , H_{N-1}$ 들이
- sample space $S$의 partition(전부 모이면 $S$를 이룸)이면서,
- $P(H_i) >0$ 을 만족하고,
- Event $E$가 sample space $S$의 임의의 Event이며 $P(E)>0$이면 다음이 성립.
$$\begin{aligned}P(H_i|E)&=\frac{P(H_i)P(E|H_i)}{\displaystyle \sum^{N-1}_{i=0}P(H_i)P(E|H_i)} \\ &=\frac{P(H_i)P(E|H_i)}{P(E)}\end{aligned}$$
위의 식이 Bayes's theorem임.
Bayes’s Theorem은
- conditional probability 를 확장하여
- Posterior probability (사후확률, $P(H_i|E)$)를 구함.
2024.04.17 - [.../Math] - [Math] Conditional Probability and Joint Probability
[Math] Conditional Probability and Joint Probability
Conditional Probability (조건부 확률)Event $F$가 발생한 조건 하에 Event $E$가 발생할 확률이 바로 conditional probability임.$$p(E|F)=\dfrac{p(E,F)}{p(F)}$$조건에 의해, sample space가 변함. 조건에 의해 변화된 sample spa
dsaint31.tistory.com
위의 수식으로 애기한다면,
- $P(E|H_i)$ (=likelihood), $P(H_i)$ (=prior), $P(E)$ (=evidence)를 가지고
- $P(H_i|E)$ (사후확률, posterior probability)를 계산한다
보통은 $P(E)$ 는 관측 시점에 상수로 처리 가능하고,
정확한 값을 구하기 어려운지라...
잘 사용하지 않는다 (많은 경우 생략가능함).
Bayes' Theorem에서
- 새로운 사건(or 근거) 혹은 관측값 ($E$)가 발생한 경우,
- 가설 $H_i$ (Hypothesis에서 따옴)가 True(참)일 확률은
- 사전 확률 $P(H_i)$에서 사후 확률 $P(H_i|E)$로 변화 한다.
즉, Bayes' Theorem은
- 특정한 사건($E$)이 발생한 후,
- 해당 사건과 관련된 가설 $H_i$가 True(참)일 Prior(사전확률) $P(H_i)$ 과
- 우도(Likelihood) $P(E|H_i)$를 이용하여
- Posterior(사후 확률) $P(H_i|E)$를 구할 수 있음을 말함.
2022.06.02 - [.../Math] - [ML] Likelihood (우도, 기대값)
[ML] Likelihood (우도, 기대값)
Likelihood (우도) : 더보기likelihood는 probability처럼 가능성을 나타낸다는 비슷한 측면도 있으나 다음과 같은 차이가 있음.probability처럼 likelihood는 상대적 비교는 가능 (즉, likelihood가 클수록 해당 even
dsaint31.tistory.com
참고: Bayes' Theorem과 Maximizaton a Posterior Estimation (MAP 추정 알고리즘)
MAP는 Bayes' Theorem의 Posterior를 최대화(엄밀히는 posterior를 최대화하는 point estimation)하는 추정 알고리즘임.
기존의 MLE와는 다음의 차이를 보임.
Maximization Likelihood Expectation (MLE) 알고리즘의 경우, Likelihood 만을 사용하고,
Maximization a Posterior (MAP) 알고리즘의 경우, Likelihood와 Prior 를 같이 사용함.
Regression model(linear model or Neural Network)에서
- 출력값과 Label에서의 오차(error)가 Normal distribution ( $\mathcal{N}(0,\sigma^2)$을 따른다고 가정하고
- MSE를 objective function으로 사용하여 해당 모델을 학습시킬 경우, 이는 MLE와 일치함.
- 출력값과 Label에서의 오차가 Laplace distribution ($\mathcal{L}(0,b)$)를 따른다고 가정하고
- MAE를 objective function으로 사용하여 해당 모델을 학습시킬 경우, 이는 MLE와 일치함.
- 이는 Normal distribution을 가정하고 MSE를 사용한 앞서의 경우보다 outlier에 보다 강건함.
- 오차분포가 $|r| \le \delta$인 영역에서는 Normal distribution을 따르고, $|r|> \delta$인 영역에서는 Laplace Distribution이라면
- Huber Loss를 사용하여 해당 모델을 훈련시, 이는 MLE (정확히는 Robust Likelihood Model)에 일치함
- 이는 앞서 두가지 경우의 절충임.
여기에 데이터(정확히는 모델의 출력과 label의 차이) 뿐 아니라, 모델 파라미터에 Prior를 도입하면 MAP가 된다.
- error는 Normal distribution을 따르면서, 모델 파라미터가 $\mathcal{N}(0,r^2)$를 따른다는 prior도입할 경우, 이는 MAP estimation 에 해당함.
- 이 같은 MAP추정은 RIDGE regression (MSE Loss + L2-Norm Regularization)과 일치함.
- error는 Normal distribution을 따르면서, 모델 파라미터가 $\mathcal{L}(0,b)$를 따른다는 prior도입한 MAP estimation의 경우엔
- LASSO regression (MSE Loss + L1-Norm Regularization)과 일치함.
- error가 Normal distribution을 따르면서, 모델 파라미터가 $p(\theta) \propto \exp\left( -\lambda \left( \alpha \|\theta\|_1 + (1-\alpha) \|\theta\|_2^2 \right) \right)$ 의 prior (mixed distribution)를 따를 경우엔
- Ridge regression 과 Lasso가 혼합된 ElasticNet과 일치함.
https://dsaint31.me/mkdocs_site/ML/ch01/ch01_41/?h=elastic#2-ridge-regression
BME
[ML] Classic Regressor (Summary) DeepLearning 계열을 제외한 Regressor 모델들을 간단하게 정리함. 분류 Instance Based Algorithm Model Based Algorithm Linear Model Linear Regression Regularization Ridge Regression Lasso Regression Elast
dsaint31.me
다음의 자료들을 참고하라.
2023.10.25 - [.../Math] - [Math] Normal Distribution (정규분포, Gaussian Distribution)
[Math] Normal Distribution (정규분포, Gaussian Distribution)
Normal DistirbutionGaussian Distribution, Laplace-Gaussian Distribution 라고도 불림. 특히, mean=0이고, std=1인 경우, Standard Normal Distribution이라고 불림.1. 정의Normal Distribution의 pdf (probability density function)는 다음과
dsaint31.tistory.com
2025.01.13 - [.../Math] - [Math] Laplace Distribution
[Math] Laplace Distribution
Laplace 분포(Laplace Distribution) 소개Laplace 분포(Laplace Distribution)는 다음과 같은 특징을 가지는 연속확률분포임.sharp한 peak(정점)(Normal Distribution에 비해 더) 두꺼운 꼬리(heavy tails)를 가짐.double exponentia
dsaint31.tistory.com
2024.11.25 - [Programming/DIP] - [Math] Maximum Likelihood Estimator: M-Estimator
[Math] Maximum Likelihood Estimator: M-Estimator
1. M-Estimator란M- Estimator는 Noise 에 Rubust 한 Statistical Estimator(통계적추정방법) 의 하나로서,Maximum Likelihood Estimatro (MLE)를 일반화한 방법임.이는 모델 parameter $\boldsymbol{\theta}$를 추정하기 위해residual $\
dsaint31.tistory.com
2. 해석
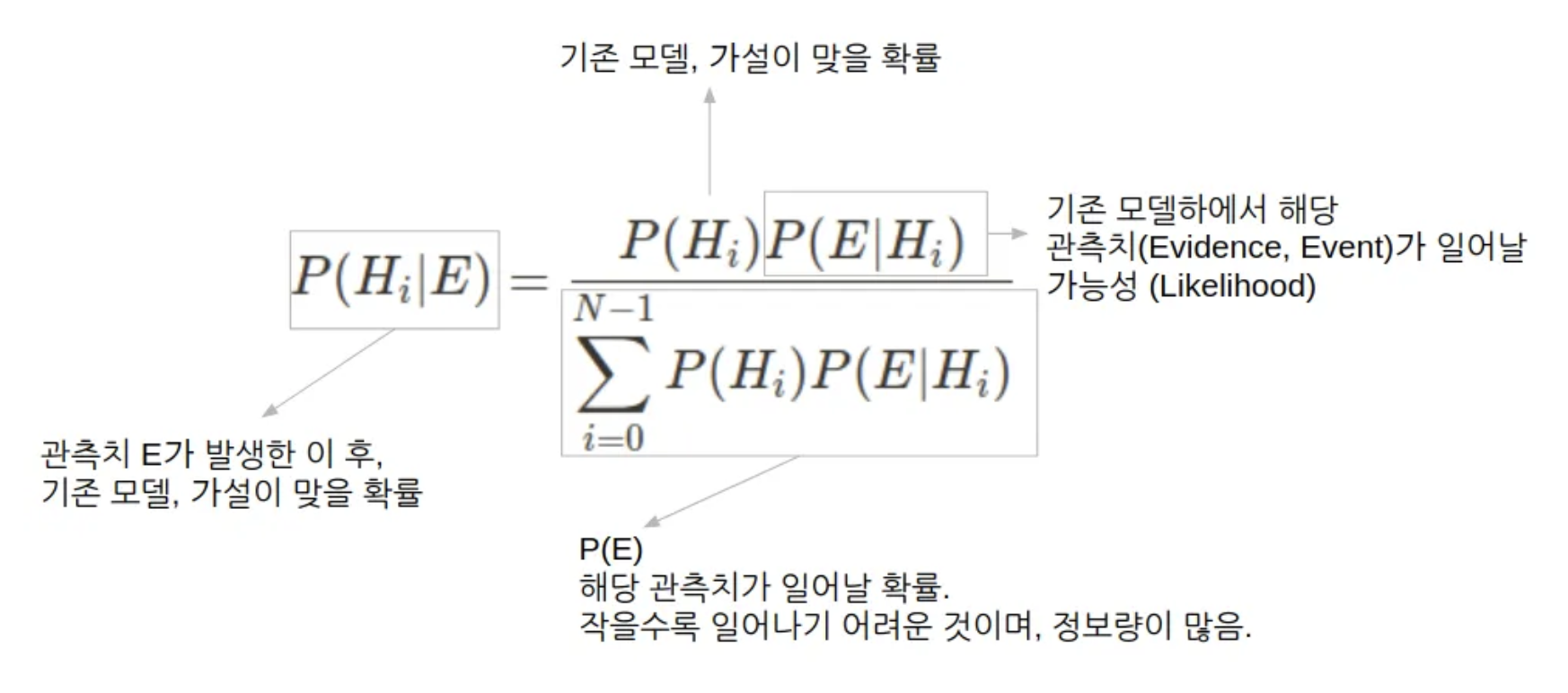
새로 발생된 (혹은 관측된) Event $E$를 통해 사후확률 $P(H_i|E)$를 구함.
이때 기존의 알려진
- 과거의 경험으로 알고있는 사전확률 $P(H_i)$와 $P(E)$,
- 그리고 Likelihood $P(E|H_i)$를 이용함.
Baye’s Theorem의 특징은,
어떤 실험 혹은 관측을 통해 얻어진 사건을 통해,
원인을 추론(혹은 기존 가설이 맞은 확률을 계산)할 수 있다는 것임.
결국, 새로운 관측 $E$를 통해 확률 $P(H_i)$에서 $P(H_i|E)$를 얻을 수 있음.
- 이전에 알고 있던 정보(prior), $P(H_i)$에
- 관측된 $E$를 통해 새로 습득한 정보인 $P(E|H_i)$를 조합
- 이를 바탕으로 사후 확률(posterior), $P(H_i|E)$를 예측
- 이 Posterior(사후 확률)로 결정을 내림.
- 이 사후 확률은 이후에는 일종의 업데이트된 사전 확률이 될 수 있음.
- 여기에 또 다른 정보가 추가되면 해당 시점의 사후 확률이 구해짐.
3. 예제들
3-1. Example 1
당신이 어떤 희귀병이 걸렸는지를 검사했는데 양성이 나왔다. 해당 희귀병의 유병률(=$P(H)$)은 1%이며 받은 검사법의 sensitivity는 95%이고 specificity도 95%라 하자. 당신이 해당 희귀병에 걸렸을 실제 확률(= $P(H|E)$)은 ?
$$\begin{aligned}P(H|E)&=\frac{P(H)P(E|H)}{P(E)}\\&=\frac{0.01\times0.95}{0.01\times0.95+0.99\times0.05}\\&\approx0.16\end{aligned}$$
해당 희귀병을 암이라고 하고 알기쉽게 그림으로 그리면 다음과 같음.
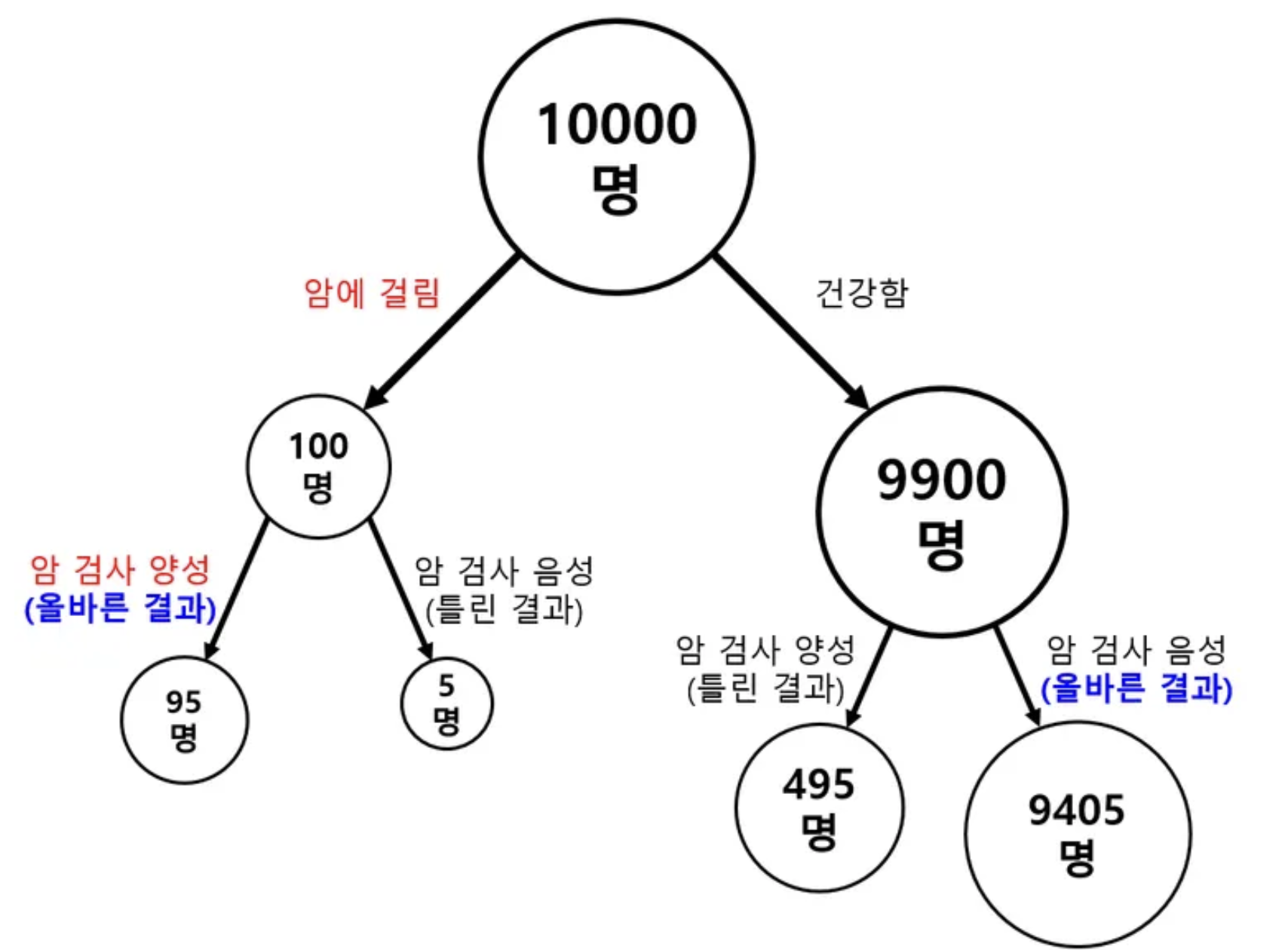
- 해당 질병 자체가 워낙 희귀하기 때문에, 실제로 안 걸린 사람이 절대 다수임.
- 검사법이 95%의 정답률을 보이지만, 실제로 안 걸린 사람들 중 5% (=495명)는 양성으로 나온다는 애기임.
- 때문에 안 걸린 사람의 5%에 해당하는 숫자(=495명)가 실제 걸린 사람들 중의 95% (95명)보다 훨씬 많은 비중을 차지하게 되므로 실제 확률은 그리 높지 않음.
- 물론 양성 판정을 받기전에는 1%였는데 16%로 늘어난 것을 무시할 수는 없음. ▶ 보다 정밀한 검사가 필요한 이유임.
3-2. Example 2
라면을 맛보고 스프를 먼저 넣었는지 면을 먼저 넣었는지를 90%의 확률로 구분할 수 있는지에 대한 예
Likelihood (우도) 에서 Posterior Probability를 통해 어떤 가설이 맞는지를 구분할 수 있음.
- $H_0$ : 구분을 못한다는 가설. 이 경우 한번의 trial에서 정답을 맞출 확률은 $P(E_1|H_0)=0.5$임.
- $H_1$ : 90%의 정확도로 구분한다는 가설. 이 경우 한번의 trial에서 정답을 맞출 확률 $P(E_1|H_1)=0.9$임.
5번 연속으로 맞춘 관측치($E_5$)가 있다면, $P(E_5)$는 다음과 같음.
$$\begin{aligned} P(E_5) &=\displaystyle \sum^{1}_{i=0} P(H_i)P(E_5|H_i) \\ &=P(H_0)P(E_5|H_0)+P(H_1)P(E_5|H_1) \\ &= 0.5 \times 0.5^5+0.5\times 0.9^5 \\ &=0.3105 \end{aligned}$$
- Law of Total Probability를 참고할 것.
- 알아맞출 수 있을지 없을지를 처음에는 모른다고 가정하면 각 가설이 참일 확률은 모두 0.5임.
- $P(H_0)=P(H_1)=0.5$
- Baysian의 관점에서 이는 나의 현재 믿음(or지식)이라고 볼 수 있음.
- 즉, prior probability임.
- $P(H_0)=P(H_1)=0.5$
- 알아맞출 수 있을지 없을지를 처음에는 모른다고 가정하면 각 가설이 참일 확률은 모두 0.5임.
- 각 가설의 Posterior Probability는 다음과 같음.
$$\begin{aligned}P(H_0|E_5)&=\frac{P(H_0)P(E_5|H_0)}{P(E_5)}\\&=\frac{0.5\times0.031}{0.3105}\\&\approx0.05\end{aligned}\\ \begin{aligned}P(H_1|E_5)&=\frac{P(H_1)P(E_5|H_1)}{P(E_5)}\\&=\frac{0.5\times0.59}{0.3105}\\&\approx0.95\end{aligned}$$ - 일반적으로 분모 $P(E_5)$는 구하기 어려운 경우가 많음.
- 때문에 분자의 Prior와 Likelihood간의 곱만으로 판정을 내리는 경우가 대다수임.
- 모든 경우의 prior와 likelihood를 구하고 나서 더하면 $P(E_5)$가 됨
분모인 $P(E_5)는 보통 Law of Total Probability로 구해짐: 2024.04.23 - [.../Math] - [Math] The Law of Total Probability
[Math] The Law of Total Probability
The Law of Total Probability (전확률의 법칙) $E_0, E_1, ... , E_{N-1}$이 sample space $S$의 partition이고,$P(E_i)>0$이면 다음이 성립$$P(A)=\displaystyle \sum^{N-1}_{i=0}P(B_i)P(A|B_i)$$위가 성립하는 것을 Law of Total Probability라
dsaint31.tistory.com
3-3. Example 3
이 예제는 오일석 교수님의 기계학습에서 나온 것입니다: 한글 책으로 이론에 가장 충실한 책중 하나라고 생각함.
https://product.kyobobook.co.kr/detail/S000001743455
기계 학습 | 오일석 - 교보문고
기계 학습 | 1.기계 학습의 A부터 Z까지 폭넓게 다루고, 특히 딥러닝을 깊이 있게 설명한다. 2.어렵고 방대한 주제이지만 친절하고 자세하게 설명해서 입문자를 배려한다. 3.다양한 그림과 예제,
product.kyobobook.co.kr
아래 그림과 같이 “주머니에서 카드를 뽑아 상자를 선택하고 선택된 상자에서 공을 뽑아 관찰”하는 확률 실험을 생각하자.
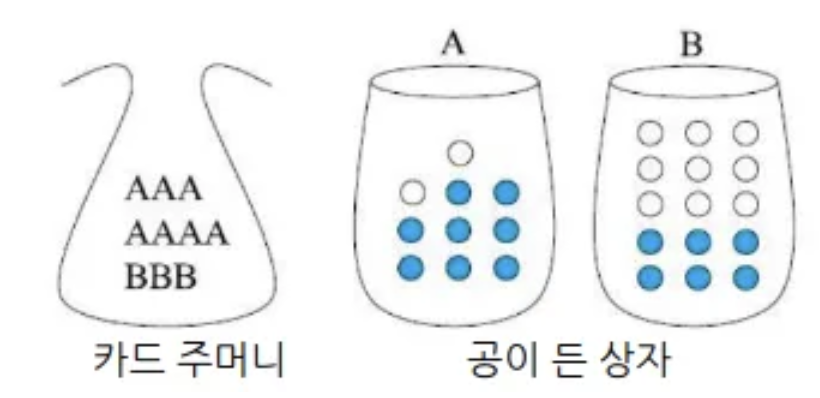
만약 흰 공이 뽑힌 사건이 발생하는 경우, 해당 공이 어느 상자에서 나왔는지 알아맞추시오.
정확히 비교해야 할 값은 사후 확률 Posterior Probability는 다음과 같음.
- $P (x=A | b=W) = P(A|W)$
- $P (x=B | b=W) = P(B|W)$
이 경우, 특정 상자가 뽑힐 확률 P(x)는 다음과 같음.
- $P(x=A) =P(A) = 0.7$
- $P(x=B) =P(B)= 0.3$
$P(x)$는 문제에서 사전 확률(흰공이 뽑히기 전에 정해진 확률임)이라 할 수 있음.
특정 상자(X)에서 흰공이 나올 조건부 확률 $P(b|x)$
- 상자 A에서 하얀공이 뽑힐 조건부 확률: $P(b=W|x=A) =P(W|A) = 0.2$
- 상자 B에서 하얀공이 뽑힐 조건부 확률: $P(b=W|x=B) =P(W|B) = 0.6$
위의 두 조건부 확률은 특정 상자에서 흰 공이 나올 확률로서 우도(likelihood, 특정 값을 얻을 확률)라고 불림.
Sol I : 상자 A가 뽑힐 확률과 상자 B가 뽑힐 확률을 비교하여 큰 쪽을 택함. (사전 확률 $P(x)$를 이용)
$P(A)=0.7 > P(B)=0.3$
- 만약, $P(W|B)=0.99$라면 prior만 가지고 판단을 내리는게 타당하다고 볼 수 있을까?
- 답은 없음...
Sol II : 흰 공이 선택되었으므로, 상자 A에서 흰 공이 나올 확률과 상자 B에서 흰 공이 나올 확률을 비교하여 큰 쪽을 택함. (조건부 확률 $P(b=W|x)$, 즉 likelihood를 이용.)
$P(W|A)=0.2 < P(W|B)=0.6$
- likelihood를 사용해서 구분할 경우, P(A)= 0.9999라면 타당한가?
- 답은 타당하지 않음.
Sol III : Posterior Probability
$$
P(A|W)=\dfrac{0.7 \times 0.2}{0.7\times 0.2 + 0.3 \times 0.6}=\dfrac{0.14}{0.14+0.18}=0.4375 \\ P(B|W)=\dfrac{0.3 \times 0.6}{0.7\times 0.2 + 0.3 \times 0.6}=\dfrac{0.18}{0.14+0.18}=0.5625
$$
즉, B상자에서 나왔다고 봐야함.
3-4. Example 4: Monty Hall Problem
세 개의 문 중에 하나를 선택하여 문 뒤에 있는 선물을 가질 수 있는 게임쇼에 참가했다.
한 문 뒤에는 자동차가 있고, 나머지 두 문 뒤에는 염소가 있다.
이때 어떤 사람이 예를 들어 1번 문을 선택했을 때, 게임쇼 진행자는 3번 문을 열어 문 뒤에 염소가 있음을 보여주면서 1번 대신 2번을 선택하겠냐고 물었다. 이때 원래 선택했던 번호를 바꾸는 것이 유리할까?
(단, 게임쇼 진행자는 정답을 알고 있으며 반드시 염소가 있는 문만을 열어준다.)
https://johngrib.github.io/wiki/Monty-Hall-problem/
몬티 홀 문제(Monty Hall problem)
johngrib.github.io
3-5. Example 5
신종 플루에 대한 좋은 검사법이 있어서 병에 걸린 사람의 경우 이 검사는 99% 양성 반응(sensitivity,power)을 나타낸 반면, 건강한 사람의 2%정도(1-specificity)도 양성반응을 보인다고 가정하자. 만약 당신이 양성반응을 보였다면 실제로 H1N1 병에 걸렸을 확률은 얼마일까? (단, 신종플루가 1000명당 한 명 걸린다는 믿을 수 있는 통계가 있다고하자.)
- $P(H)=0.1$ : 신종 플루에 걸릴 확률 (0.1%)
- $P(E|H)=0.99$ : 신종 플루시 양성반응이 나올 확률 (99%)
- $P(E)$ : 양성반응이 나올 확률 (2.09%) ← The Law of Total Probability
$$P(H|E)=\frac{P(H)P(E|H)}{P(E)}=\frac{0.001\times 0.99}{(0.001\times 0.99)+(0.999 \times 0.02)}\approx0.047$$
해당사람이 검사를 받기 전엔 0.001의 확률(사전확률)로 신종 플루에 걸릴 확률이었지만, 양성반응이라는 관측치에 의해 확률(사후확률)이 0.0472로 올라 간 것을 볼 수 있음.
4.7%이므로 양성 반응이지만 지나친 걱정을 하지 않아도 된다고 볼 수 있음. 단, 사전확률과 비교하여 사후확률의 증가비를 고려해서 추가적인 검사를 하는게 합리적임.
같이보면 좋은 자료들
2024.04.17 - [.../Math] - [Math] Probability 란: Probability, Odds, Likelihood
[Math] Probability 란: Probability, Odds, Likelihood
Probability란 ? 어떠한 event(사건, 사상)의 공간(=sample space, 발생가능한 모든 sample points로 구성된 set)에서특정 event(or sample point의 set으로 sample space의 subset)가 선택될(발생할) 수 있는불확실성(uncertain
dsaint31.tistory.com
'... > Math' 카테고리의 다른 글
| Error Propagation (or Delta Method) (0) | 2025.10.08 |
|---|---|
| sampling error vs. sampling bias (0) | 2025.09.16 |
| [Summary] 확률 및 통계 기본 (0) | 2025.05.08 |
| [Math] Gamma Function (0) | 2025.04.29 |
| [Math] Gamma Distribution (링크 보완 필요) : (2) | 2025.04.29 |