Interpolation (on Image)
measure 되지 못한 or 모르는 pixel(or sample)의 값을 주변의 pixel(or sample)들을 이용하여 구하는 과정.
Given ($x_0$, $y_0$ ), ( $x_1$ , $y_1$), $\cdots$ ($x_n$, $y_n$),
find the value of $y$ at a value of $x$ that is not given
- 단, Interpolation으로 얻어진 inerpolant의 경우, 주어진 주변의 pixel 값들을 정확히 그대로 재현해야함.
- 일반적인 fitting 또는 approximation과 가장 큰 차이점이 바로 이 것임.
- 또한 interplation으로 추정되는 값들은 항상 주어진 값들의 사이에 존재한다 (extrapolation과 다름)
보간 함수(Interpolant)
- 주어진 데이터 점들 사이의 값을 추정하기 위해 사용되는 함수.
- 보간(interpolation)은 이미 알려진 데이터 포인트를 기반으로 그 사이의 미지의 값을 예측하는 과정이며,
- 보간 함수는 이 과정에서 핵심적인 역할을 수행
2024.06.13 - [Programming/DIP] - [CV] Fitting
[CV] Fitting
computer vision과 image processing에서의 Fitting목표computer vision과 image processing에서 Fitting의 주요 목표는관찰된 데이터(이미지, 텍스트, 센서 데이터 등)로부터특정 양이나 구조를가장 잘 설명하는 모델
dsaint31.tistory.com
1. Polynomial Interpolation
Polynomial Interpolation은 주어진 data points를 정확히 통과하는 polynomial function을 구하여, 주어진 data points 사이 points들을 구하는 방법.
- 이는 $n$개의 데이터 점이 주어졌을 때, 이 점들을 모두 지나는 $(n-1)$차 이하의 유일한 polynomial을 구함.
Polynomials are the most common choice of interpolations because they are easy to:
- Evaluate
- Differentiate, and
- Integrate.
2. Piecewise Polynomial Interpolation
전체 구간을 소구간별로 나누어
저차수의 polynomial (다항식)으로 interpolant를 구하는 방법
데이터 포인트들을 여러 구간으로 나누고, 각 구간별로 별도의 다항식(independent polynomials)을 적용하여 interpolation.
- 각 구간의 다항식은 독립적으로 계산되기 때문에 구간 경계에서의 연속성이 보장되지 않음.
- 구현이 비교적 간단함
- 심지어 각 구간에 대해 다른 차수의 다항식을 사용할 수도 있음.
- 구간 경계에서 불연속성이 발생할 수 있기 때문에, 전체적인 매끄러움이 떨어질 수 있다는 단점을 가짐.
3. Spline Interpolation
Piecewise Polynomial Interpolation (구간별 다항식 보간법)의 “한 종류”로,
구간 경계에서의 연속성과 매끄러움을 개선.
일반적으로 3차 다항식(cubic spline)을 사용하며, 구간 경계에서 연속성과 미분 가능성을 보장함.
Spline interpolation 은 pieceiwse polynomial interpolation 의 특별한 형태에 불과함.
- degree $k$인 polynomial을 사용시
- “$k-1$ th order continously differntialbe $C^{k-1}$”이 보장되는
- piecewise polynomial interpolation을 가리킴.
A spline is a special type of piecewise polynomial interpolation: a piecewise polynomial of degree $k$ is a spline if it is continuously differentiable $k-1$.
- 즉, 스플라인 곡선(spline curve)은 주어진 복수의 제어점을 통과하는 부드러운 곡선으로,
- Spline Interpolation은 인접한 두 점 사이의 구간마다 별도의 다항식을 이용해 곡선을 정의함.

4. B-Spline Interpolation
“기저함수의 선형조합”를 통해 Spline interpolation을 구현한 b-spline(basis spline) interpolation이 등장:
- When you write a "spline curve"
- as a linear combination of B-spline basis functions in this way,
- it's called a "B-spline".
B-Spline Interpolation 이란
Spline Interpolation의 또다른 표현법
- 다항식 외에 Radial Function(가장 유명한 예로 Gaussian이 존재)과 같은 다른 함수를 기저(basis)로 사용 하고 이를 선형조합시켜서 보간.
- Basis function의 도입을 통해 높은 차수의 연속성을 보다 효율적으로 구현 가능하며 Non-Uniform Rational B-Spline과 같은 보다 일반화된 구현이 가능.
- 단, 직관적이지 않고, control point로 쓰이는 원래 가진 데이터 포인트를 통과하지 않기 쉬워서 interpolation이라기 보다 approximation이 되기 쉬움.

And the important point is that
any piecewise polynomial (i.e. any spline) can be written as a B-Spline.
https://mathworld.wolfram.com/B-Spline.html
Wolfram MathWorld: The Web's Most Extensive Mathematics Resource
Comprehensive encyclopedia of mathematics with 13,000 detailed entries. Continually updated, extensively illustrated, and with interactive examples.
mathworld.wolfram.com
5. Polynomial vs. Piecewise Poly vs. Spline
5-1. Polynomial Interpolation
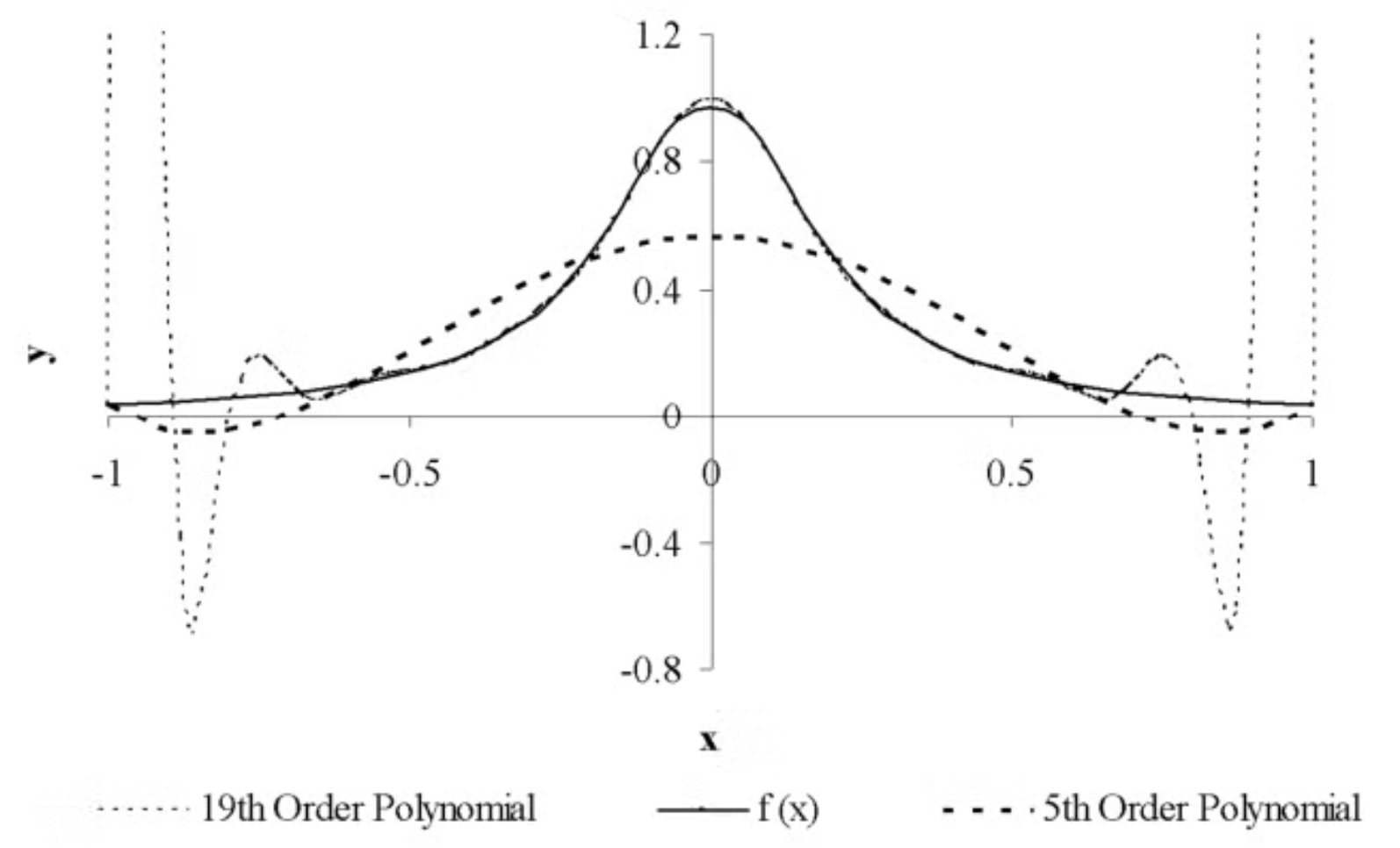
Polynomial 은 ”자연계의 현상을 모사하는 강력한 tool“이나 **“한계”**가 존재
- Taylor series 에서도 알 수 있듯이, 멀리 떨어진 위치의 값을 예측할 경우 오차가 커짐.
- Higher order polynomial interpolation is a bad idea!!
5-2. Piecewise Polynomial Interpolation
이를 보완하기 위해 piecewise polynomial interpolation등장 :
- 가급적 가까운 값들만을 예측하도록 경계를 나누어 처리.
- 즉, 작은 구간으로 여럿 나누고 개별 경계마다 polynomial을 계산.
- 단점은, 다른 구간 둘이 만나는 구간경계에서의 연속성과 매끄러움이 보장되지 못함
5-3. Spline Interpolation
이를 보완한 Spline interpolation이 등장
- k-th porder splined의 경우, $C^{k-1}$ 이 보장되는 k-th order polynomial.
- 이를 통해, 구간경계에서의 연속성과 매끄러움이 보장됨.
6. Image 에서 많이 사용되는 Interpolation Algorithms
6-1. Nearest Neighbor Interpolation (NN)
Zero order spline interpolation 이라고도 불림.
- 가장 가까운 pixel의 값으로 estimation.
- 빠르지만, 영상의 질이 좋지 못함.
6-2. Bilinear Interpolation (linear)
First order (spline) interpolation
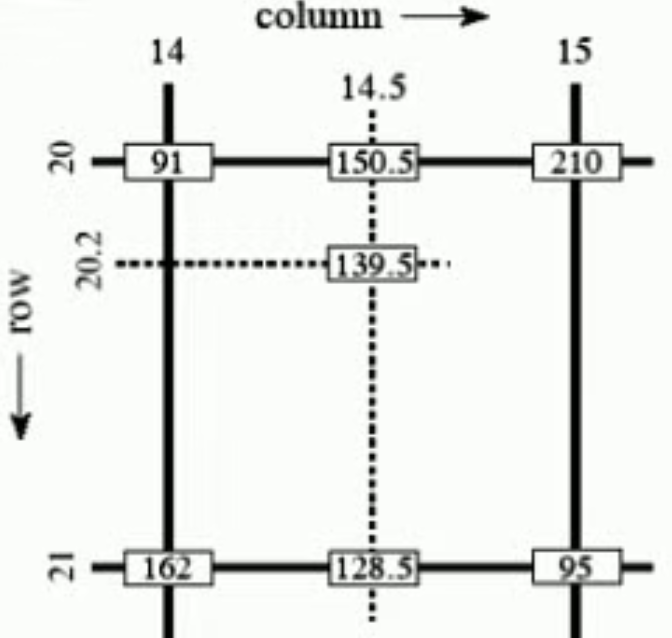
Let $(x,y)$ denotes the coordinates of the location to which we want to assign an intensity value (think of it as a point of the grid described previously), and let $v(x,y)$ denote that intensity value. For bilinear interpolation, the assigned value is obtained using the equation
$$ v(x,y)=ax+by+cxy+d \tag{2.17} $$
where the four coefficients are determined from the four equations in four unknowns that can be written using the four nearest neighbors of point $(x,y)$.
- 인접한 4개의 pixel을 이용하여 해당 intensity와 pixel과의 거리를 이용하여 estimation
- linear interpolation을 x,y축에 따로 수행한 결과임. (volume의 경우 trilinear interpolation이 됨)
6-3. Quadratic Interpolation
Second order (spline) interpolation
Given $(x_0, y_0), (x_1, y_1), \cdots ,(x_{n-1}, y_{n-1}), (x_n, y_n)$, fit quadratic splines through the data.
The spline are given by
$$ \begin{aligned}f(x)&=a_1x^2+b_1x+c_1, & x_0 \le x<x_1\\ &=a_2x^2+b_2x+c_2, & x_1 \le x<x_2\\ & \quad \quad \vdots\\&=a_nx^2+b_nx+c_n, & x_{n-1} \le x<x_n\\ \end{aligned} $$
point를 3개 사용하는 piecewise polynomial interpolation로 degree를 2로 하고 power function을 basis로 할 경우, 2nd order spline interpolation (= quadratic interpolation)임.
$$ \begin{pmatrix} 1 & x_0 & x_0^2 \\ 1 & x_1 & x_1^2 \\ 1 & x_2 & x_2^2 \end{pmatrix} \begin{pmatrix} c_0 \\ c_1 \\ c_2\end{pmatrix} = \begin{pmatrix} y_0 \\ y_1 \\ y_2 \end{pmatrix} $$
위의 matrix는 Vadermonde matrix이며, determinant는 다음과 같음.
$$ \begin{vmatrix} 1 & x_0 & x_0^2 \\ 1 & x_1 & x_1^2 \\ 1 & x_2 & x_2^2 \end{vmatrix} = (x_2-x_1)(x_2-x_0)(x_1-x_0) \ne 0 $$
determinant가 0이 아닐 경우, inverse를 구할 수 있고 solution이 exactly one (=unique)함. 즉 계수들을 유일하게 구할 수 있음.
$$ c_2 = \frac{1}{x_2-x_1} \left[ \frac{f_2-f_0}{x_2-x_0} - \frac{f_1-f_0}{x_1-x_0} \right],\\c_1 = \frac{f_1-f_0}{x_1-x_0} - c(x_1+x_0) , \\ c_0 = f_0-b x_0-c x_0^2 $$
위에서 구한 계수를 통해 interpolant를 완성.
6-4. Bicubic Interpolation
3rd-order spline interpolation
The intensity value assigned to point $(x,y)$ is obtained using the equation
$$(x,y)=\sum^3_{i=0}\sum^3_{j=0}a_{ij}x^iy^j \tag{2-18}$$
The sixteen coefficients are determined from the sixteen equations with sixteen unknowns that can be written using the sixteen nearest neighbors of point $(x,y)$.
축 하나에서 cubic interpolation 수행할 경우, 4개의 pixel을 사용함: 필요한 point 수 = $(k+1)^{a}$
- $k$ : # of degree
- $a$ : # of axes
다음의 근사식을 사용하기도 함.
$$W(x)= \left\{ \begin{matrix}(a+2)|x|^3-(a+3)|x|^2+1 & 0\le |x|<1 \\ a|x|^3-5a|x|^2+8a|x|-4a & 1 \le |x|<2 \\ 0 & 2\le |x| \end{matrix} \right. \\ \text{where, } a=-0.5, -0.75 \text{ or } -1.0$$
$|x|$ 는 distance 로서 4개의 주변 pixel은 거리에 따라 $W(x)$ 로 weighting이 되어 더해져서 target pixel의 값을 구함.
Bicubic Interpolation 은 x축과 y축에 각각 cubic interpolation이 수행되어 얻어짐 : 총 16개의 pixel이 사용됨.
6-5. INTER_AREA
2024.09.22 - [Programming/DIP] - [DIP] CV2.INTER_AREA
[DIP] CV2.INTER_AREA
CV2.INTER_AREA는 OpenCV 라이브러리에서 제공하는 image interpolation 방법 중 하나임. 주요 특징과 작동 방식은 다음과같음:목적:주로 이미지를 축소(downsampling or shrinking)할 때 사용됨.pixel area 관계를 사
dsaint31.tistory.com
7. 참고자료
https://jrjohansson.github.io/numericalpython.html: 7장 Interpolation
J Robert Johansson
Summary Numerical Python by Robert Johansson shows you how to leverage the numerical and mathematical capabilities in Python, its standard library, and the extensive ecosystem of computationally oriented Python libraries, including popular packages such as
jrjohansson.github.io
https://dsaint31.me/mkdocs_site/DIP/cv2/ch02/dip_geometric_transformation/#scaling
BME228
Geometric Transformations of Images Goals Learn to apply different geometric transformation to images like translation, rotation, affine transformation etc. You will see these functions: cv2.getPerspectiveTransform Transformations Transformation 이란? T
dsaint31.me
'Programming > DIP' 카테고리의 다른 글
| [DIP] Image 다루기: cv2-기본편 3 (Summary) (1) | 2024.09.22 |
|---|---|
| [DIP] CV2.INTER_AREA (0) | 2024.09.22 |
| [DIP] Image Morphing (Simple) (0) | 2024.09.22 |
| [OpenCV] bitwise op. (0) | 2024.09.22 |
| [DIP] Image 다루기: cv2-기본편 1 (Summary) (0) | 2024.09.22 |