728x90
728x90
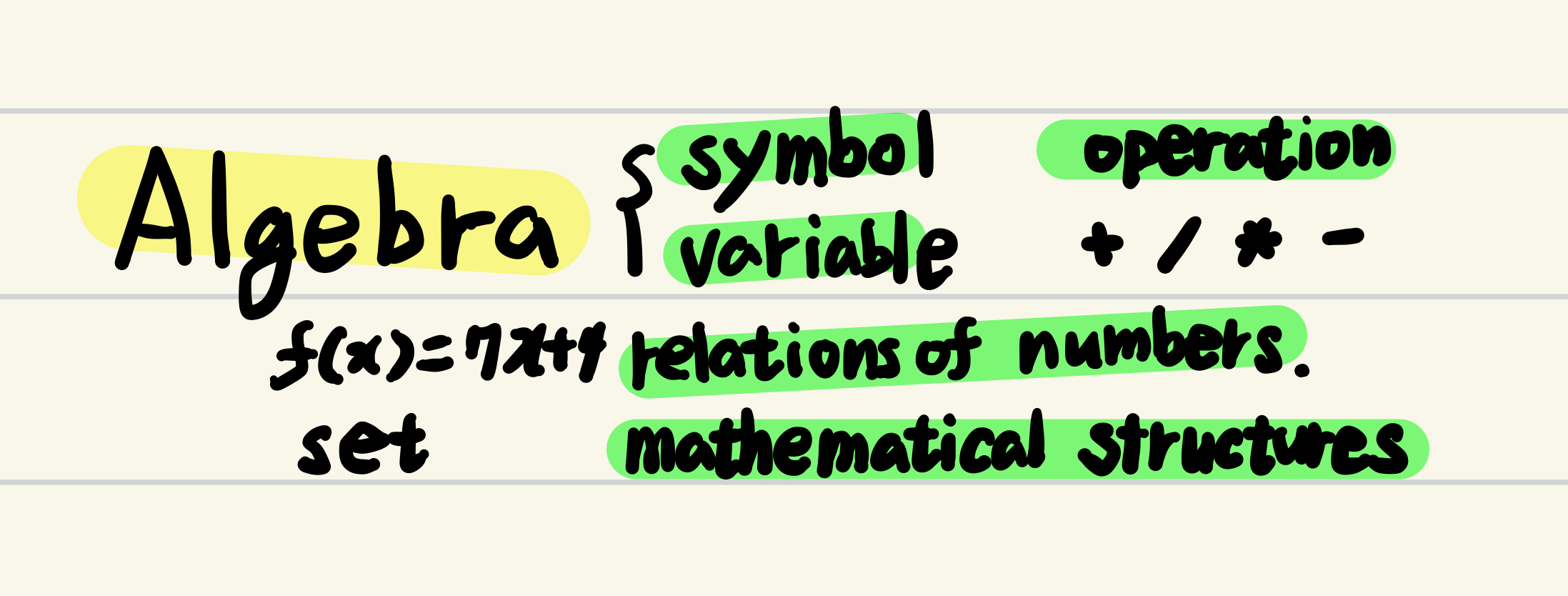
Algebra은
변수(variables)와 연산(operations)을 사용하여
수학적 구조(mathematical structures)와 관계(relationships)를
연구하고 다양한 문제를 해결하는 학문.
Definition
Algebra는
- 수와 변수를 사용하여 relation(관계)를 간결하게 표현하고,
- variable과 symbol을 통해 다양한 숫자 사이의 관계를 간단하고 일반적인 방식 (equations, inequalities 등등)으로 표시
- 특정 set(집합)과 그 구성 요소에 대한 operation rules(연산 규칙)을 연구하는 학문임.
즉, Algebra는
- 임의의 set(집합)과 그에 대한 연산 규칙 을 정의하고,
- 이를 하나의 체계(수학적 구조)로 묶어 다루는 수학의 한분야을 의미하기도 함.
- 참고로 "수학적 구조"라는 용어가 set(집합) 과 operations(연산)의 관계를 포괄적으로 나타냄.
Algebra는
Numbers 와 Symbols 를 이용하여,
수학적인 Relationships를 표현하고 조작하는
Rules(규칙)과 Structures(구조)를
연구하는 학문.
Example
대표적인 예로, Linear Algebra(선형대수학)에서 다루는 vector space(벡터 공간)을 들 수 있음.
- set of vectors(벡터의 집합)과
- 이 벡터들에 대한 두 가지 연산, 즉 vector addition(벡터 덧셈)과 scalar multiple(스칼라 곱셈)으로 구성
또 다른 예로는 Boolean Algebra도 있음.
https://dsaint31.me/mkdocs_site/CE/ch01/ch01_13_boolean_algebra/
BME228
Boolean Algebra George Boole(1815-1864, 영국)이 고안한 logic을 다루는 algebra로 "True, False를 수학적인 영역으로 포함"시켜 참과 거짓을 1,0에 대입하고, AND, OR, NOT 등의 logical operation을 사용하여 논리적 동작(
dsaint31.me
Conclusion
Algebra(대수학)은
- 다양한 종류의 algebraic structures(대수적 구조)를 다룸.
- 구조로는 groups(군), rings(환), fields(체) 등이 있음.
- 이들 각 구조는 고유한 연산 규칙과 특성을 가지고 있음
Algebra는 다양한 algebraic structure를 연구하고
그들 사이의 관계를 탐구하는 학문으로
이를 통해 복잡한 수학적 문제를 모델링하고,
최적화 문제를 해결하는 등의 다양한 분야에 응용될 수 있음.
https://dsaint31.github.io/math/math-week01/#algebra-and-operations
[Math] Week 01
Basic
dsaint31.github.io
728x90
'... > Math' 카테고리의 다른 글
| [Math] Algebraic Properties (0) | 2024.07.20 |
|---|---|
| [Math] Identity (항등원) and Inverse (역원) (0) | 2024.07.20 |
| [Math] Quaternion (사원수) 와 3D Rotation (0) | 2024.07.09 |
| [Math] Projective Space: $\mathbb{P}^n$, n차원 투영공간 (0) | 2024.07.06 |
| [Math] Hypothesis Testing 에서 Conservative Approach (보수적 접근법)란? (1) | 2024.07.05 |