David Wolpert 와 William Marcready의 1997년 논문 "No Free Lunch Theorems for Optimzation"에서 제시됨.
NFLT라는 abbreviation으로도 많이 사용된다.
이 논문에서 기술한 내용을 그대로 살펴보면 다음과 같다.
We have dubbed the associated results “No Free Lunch” theorems
because they demonstrate that
if an algorithm performs well on a certain class of problems
then it necessarily pays for that with degraded performance on the set of all remaining problems.
특정한 문제에 최적화된 알고리즘은 다른 문제들에서는 오히려 성능이 떨어진다는 것을 NFLT는 가르킨다.
ML의 경우, dataset으로부터 스스로 task를 해결하기 위한 rule을 찾아낸다. 특정 ML 알고리즘이 어떤 가정이 성립하고 있는 특정 dataset에서 task에 대해 우수한 성능을 보인다면, 해당 가정이 성립하지 않는 dataset에서는 오히려 떨어지는 성능을 보임을 NFLT은 애기한다. 모든 ML Algorithm은 철저히 Dataset에 종속되며 특정 가정이 성립하는 Dataset에 적합한 ML Algorithm은 해당 가정이 성립하지 않는 경우엔 높은 성능을 기대할 수 없다.
ML Algorithm에서 Deep Learning Algorithms을 예를 든다면 다음과 같이 이해할 수 있다.
- CNN의 경우 Locality of pixel dependency 및 stationarity of statstics라는 가정이 성립하는 dataset (= image data)에서 최적으로 동작하지만, 이들 가정이 성립하지는 않는 2D data에서는 낮은 성능을 보이게 된다.
- RNN의 경우는 현재 같은 data sample이라도 앞서 입력된 data samples가 다른 경우에는 출력이 달라지는 dataset에서 동작하는 것을 가정하고 있기 때문에 instantaneous system을 모사해야하는 경우엔 적절치 못하다.
NFLT를 달리 애기하면 세상의 모든 problem들에 대해 ML Algorithm들은 동등한 평균 성능을 가진다고 할 수 있다.
이같은 관점에서 NFLT 를 Goodfellow는 다음과 같이 설명한다.
Averaged over all possible data-generating distributions,
every classification algorithm has the same error rate
when classifying previously unobserved points.
보다 직관적인 다음의 설명도 있다.
Any two algorithms are equivalent
when their performace is averaged across all possible problems
여기서 중요한 건 평균이 같다는 것이다.
특정분야에서 뛰어나다면 나머지 다른 분야에서는 뒤떨어지는 성능을 보인다.
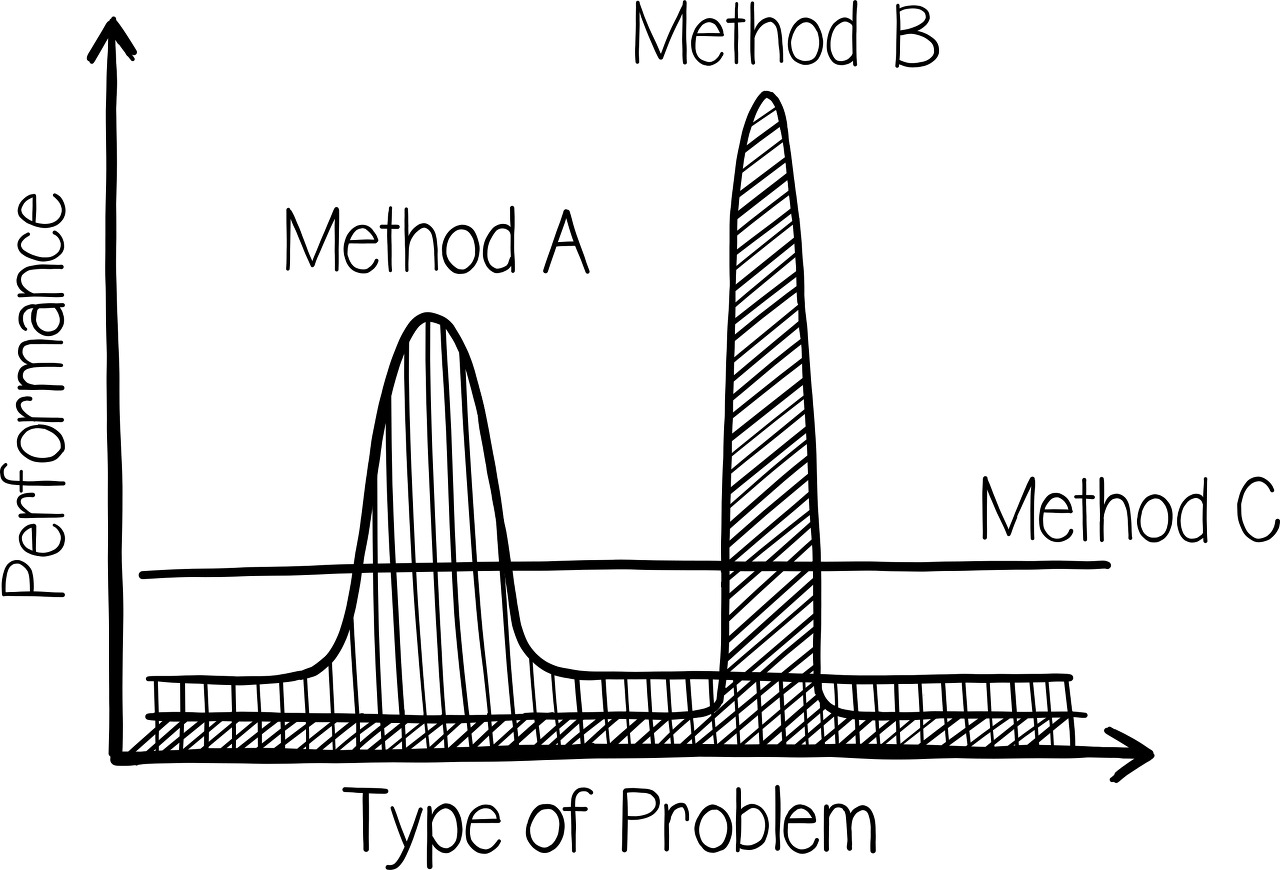
NFTL을 David Wolpert의 1976년 논문인 "The Lack of A Priori Distinctions Between Learning Algorithms"의 내용으로 설명한다면 우리가 현재 다루어야하는 dataset에 대해 어떠한 가정도 할 수 없다면(=다시 말하면 해당 데이터의 특성을 전혀 모르는 경우 또는 type of problem을 전혀 모르는 경우), 어떤 ML model이 잘 동작할지 알 수 없다는 것이다.
(달리 말하면, 어떤 경우에 대해서도 보다 나은 성능을 보이는 최고의 ML Algorithm, 즉 Universaly Best Algorithm 이란 없다는 애기다.)
이를 다르게 해석할 수도 있다.
특정한 가정들이 현재 다루는 Dataset에서 성립한다면, 해당 가정에 가장 적절한 ML Algorithm을 고를 경우 높은 성능을 기대할 수 있다. 결국 다루는 Datast의 특성을 잘 파악해야만 성립하는 가정들을 추출할 수 있고 이를 통해 최적의 ML Algorithm 또는 ML model을 고를 수 있다.
결국, ML 또는 DL을 적용하여 문제를 해결하려면, 해당 문제에 대한 이해와 함께 다루어야 하는 dataset에 대한 이해를 깊게 해야하고, 해당 이해를 바탕으로 최적의 ML Algorithm을 골라야한다.
물론, non-linear한 특성을 가지고 있는 복잡한 real world problem 의 경우, linear model 과 같이 비현실적인 가정에 기반하거나 매우 적은 자유도의 단순한 model 보다 Deep Learning Algorithm들이 보다 적절한 선택이라고 할 수 있다.
이 글을 읽고 다음의 Youtube 설명을 본다면 좀 더 쉽게 이해할 수 있을 듯하여 첨부한다.
References
- Wolpert, D.H., Macready, W.G. (1997), No Free Lunch Theorems for Optimization, IEEE Transactions on Evolutionary Computation 1, 67. http://ti.arc.nasa.gov/m/profile/dhw/papers/78.pdf
- Wolpert, D.H., “The Lack of A Priori Distinctions Between Learning Algorithms,” Neural Computation 8, no. 7 (1996): 1341–1390. https://direct.mit.edu/neco/article-abstract/8/7/1341/6016/The-Lack-of-A-Priori-Distinctions-Between-Learning?redirectedFrom=fulltext
'Computer' 카테고리의 다른 글
| [Etc] A Mathematical Theory of Communication - Claude Shannon (0) | 2025.03.08 |
|---|---|
| [DL] Keras를 위한 Scikit-Learn Wrapper : Scikeras (1) | 2023.11.13 |
| [ML] Time Series 란? (0) | 2023.09.01 |
| [Keras] 현재의 Learning Rate를 확인하는 Custom Callback (0) | 2023.08.30 |
| [DL] Hyperbolic Tangent Function (tanh) (0) | 2023.08.13 |