Modulation Transfer Function (MTF)
MTF can be defined as the magnitude of the Fourier transform of the point or line spread function.
- 입력신호가 어떤 장치-시스템을 통과하고 난 후 그 물리적 특성이 어떻게 변하는지를 나타내는 전달함수(Transfer Function : FT of Impulse Function)의 일종
- 시간(공간) domain에서 impulse response를 convolution하므로, frequency domain에서의 transfer function은 곱해짐.
주기신호(or 주기적으로 pixel intensity가 변하는 영상)를 이용하여
특정 영상시스템의 해당 신호의 modulation Transfer Function (MTF)을 구하면,
이 MTF을 통해, 해당 영상시스템의 contrast를 정량적으로 평가할 수 있음.
MTF를 이해하기 위해, 우선 modulation을 설명한다.
Modulation
"특정 신호 자체의 contrast를 정량적으로 나타낸 값"이라고 생각할 수 있음.
Modulation $m_f$의 수식은 다음과 같음.
$$m_f = \frac{f_\text{max} - f_\text{min}}{f_\text{max} + f_\text{min}}$$
- $f_\text{max}$ : 입력 주기신호에 대한 최대값.
- $f_\text{min}$ : 입력 주기신호의 최소값.
의미를 조금 풀어서 살핀 수식은 다음과 같음.
$$m_f = \frac{ \frac{f_\text{max} - f_\text{min}}{2}} {\frac{f_\text{max} + f_\text{min}}{2}}$$
- 분모는 입력 주기신호의 평균값이고, 분자는 해당 신호가 가지는 가장 큰 차이값임.
- 평균값에 대해 가장 큰 차이값이 어느 정도의 비(ratio)를 가지는지를 나타내는 것이 modulation이며, 이 값이 클수록 해당 신호는 차이가 큰 신호로 최대값과 최소값의 구분이 쉬운 신호, 즉 contrast가 높은 신호로 생각할 수 있음.
즉, modulation은 주기신호가 자신의 평균값에 대해 얼마나 contrast를 가지고 있는지를 나타냄.
- 해당 주기신호가 음수값을 가지지 않는다고 하면 modulation은 항상 $[0,1]$을 range로 가짐.
- modulation이 0인 경우, contrast가 없는 주기신호가 됨.
- average가 높은 경우 (모든 pixel에 일정한 값을 더해줄 경우 평균이 올라감), 분모가 커져 modulation이 작은 값을 가짐(contrast 감소)
다음 그림은 modulation에 따라 영상의 contrast가 어떤지를 정성적으로 보여줌.

Modulation Transfer Function (MTF)
특정 영상시스템에서 입력신호의 modulation과 출력신호의 modulation의 비.
- modulation이 특정 주기(or 주파수 $f=\frac{1}{T}$의 신호에 대해 정해지므로, MTF는 주파수(or 주기)에 따라 다른 값을 가지게되어 주파수에 대한 함수로 표현됨 (nonisotropic system에서는 orientation도 독립변수로 주어짐).
- 영상시스템에서 MTF는 공간주파수에 대한 함수로 표현되며, "해당 공간주파수 성분이 해당 영상시스템에 의해 얼마나 degradation(나빠지는지)이 이루어지는지"를 나타냄 (MTF는 $[0,1]$를 range로 가짐)
MTF의 수식은 다음과 같음.
$$\text{MTF}(u)=\dfrac{m_\text{o}}{m_\text{i}}=\dfrac{|H(u)|}{|H(0)|}$$
- $H(u)$ : $H$는 impulse response $h(x)$에 대한 Fourier transform (=Frequncy Response)이며 주파수에 대한 함수임. frequncy $u$에 해당하는 성분이 전체 impulse response에 얼마나 기여하는지를 나타냄 .
- $H(0)$ : DC성분(주파수가 0인 성분)이 전체 impulse reponse에 얼마나 기여하는지를 나타냄.
- $| \cdot |$ : $\cdot$에 보통 어떤 함수가 들어가며, 해당 함수의 magnitude를 애기함 (간단한 예로 절대값을 들 수 있음.)
- $m_\text{o}$ : 출력 신호의 modulation, 해당 출력신호는 주파수가 $u$임.
- $m_\text{i}$ : 입력 신호의 modulation, 해당 입력신호는 주파수가 $u$임.
영상에서는 impulse reponse로 Point Spread Function(PSF)이 사용되므로, 영상시스템의 MTF에는 해당 시스템의 PSF가 영향을 줌.
다음 그림은 특정 축에 대해 주기성을 가지는 입력영상을 통해 MTF를 구한 것이라고 생각할 수 있음
(보통 단순히 하기 위해 영상시스템이 circularly symmetric한 PSF를 갖는다고 생각하면 모든 축에 대해 MTF가 동일)

- DC성분과 낮은 공간주파수 성분은 해당 시스템에서 degradation이 일어나지 않고 출력에 기여하지만...
- $0.6mm^{-1}$이후로는 contrast가 매우 떨어지게 되는 것을 확인할 수 있음. (modulation이 절반 이하로 감소)
- 대부분의 영상시스템이 고주파 성분에서 degradation이 발생하는 MTF를 가짐. (고주파에서 높은 MTF를 가진다는 건 출력영상이 높은 공간해상도에서 높은 contrast를 가짐을 의미.)
다음 그림은 MTF를 잘 나타낸 그림이다. (Imaging lens를 영상시스템으로 생각해도 됨.

MTF와 Spatial Resolultion
같은 shape의 MTF에서는 cut-off frequency를 통해 spatial resolution의 비교가 쉽게 가능하다.
하지만, 다음과 같이 MTF의 모양이 다른 경우엔 복잡하다.
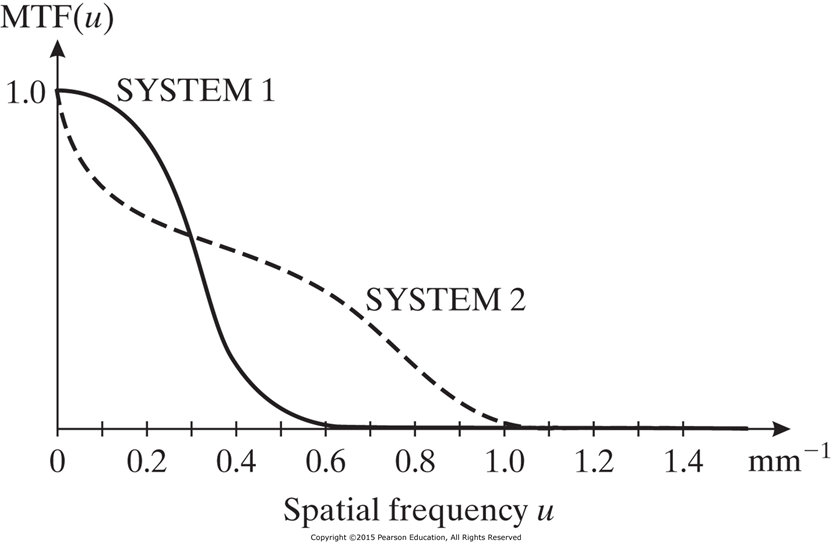
- 시스템 1은 낮은 공간주파수 성분에서는 contrast가 우수하므로 coarse detail이 시스템2보다 좋다.
- 시스템 2는 높은 공간주파수 성분에서 contrast가 우수하고, 이는 fine detail을 나타내는데 장점을 가진다.
공간해상도는 MTF로 파악을 할 수는 있지만, 위와같은 이유로 PSF나 LSF (=시스템의 impulse response)의 FWHM로 나타내는게 훨씬 편하다.
일반적으로는 높은 공간주파수에서 큰 값을 가지면서 높은 cut-off frequency를 가지는 MTF에 해당하는 영상시스템이 보다 공간해상도가 좋다고 볼 수 있다.
References
https://www.amazon.com/Medical-Imaging-Signals-Systems-2nd/dp/0132145189 : 3.2 Contrast
Amazon.com
Enter the characters you see below Sorry, we just need to make sure you're not a robot. For best results, please make sure your browser is accepting cookies.
www.amazon.com
https://www.dxomark.com/glossary/mtf-2/
MTF - DXOMARK
Modulation Transfer Function) curve, Function describing the ratio between the amplitude of a pure frequency signal before and after a system as a function of the frequency. Indicates the ability of a film to record fine detail.
www.dxomark.com
'Programming > DIP' 카테고리의 다른 글
| [DIP] Full Width at Half Maximum (FWHM) (1) | 2022.09.26 |
|---|---|
| [DIP] Local Contrast (1) | 2022.09.26 |
| [DIP] OpenCV 에서 URL로 이미지 로딩 (0) | 2022.09.21 |
| [DIP] Color Space or Color Model (0) | 2022.09.21 |
| [OpenCV] cv2.cvtColor (0) | 2022.07.14 |