728x90
728x90
Odds란?
$$\text{Odds} = \frac{p}{1-p}$$
where
- $p$is the probability of belonging to class of $1$ (success).
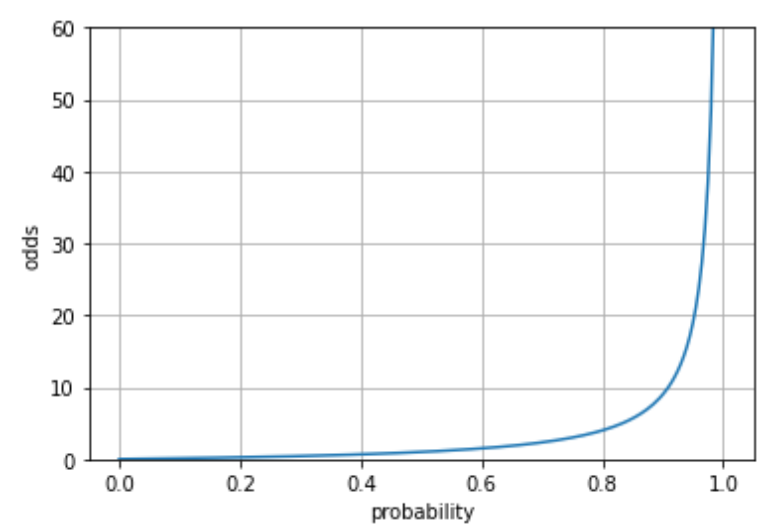
특징
odds의 range는 $[0,\infty]$ 임. (symmetric)
probability가 $[0,1]$ 것과 차이가 있음.
- 어떤 event가 일어날 가능성에 대한 정량적 정보를 제공하나, probability와는 다름.
- likelihood, odds, probability 모두 어떤 event가 일어날지에 대한 정량적 비교는 가능하나 조금씩 차이가 있음.
- case control study에서 매우 probability가 낮은 경우에 대한 risk ratio를 odds ratio가 대체하기도 함.
- risk ratio $RR=\frac{p(event|exposed)}{p(event|unsxposed)}=frac{p_1}{p_0}$는 Cohort study에서만 계산 가능함.
- 하지만 probability가 매우 낮은 경우 $1-p \approx p$가 성립하므로
- odd ratio $OR=\frac{\frac{p_1}{1-p_1}}{\frac{p_0}{1-p_0}}\approx \frac{p_1}{p_0}$가 risk ratio를 근사 가능.
- Case-Control은
- **결과(질병 유무)**를 기준으로 사람을 먼저 나누고,
- 그 다음에 과거의 노출 여부를 조사하는 후향적 연구.
- 이 때문에 전체 모집단에서 질병 발생 확률 자체를 추정할 수 없음.
- 하지만, 질환의 probability가 낮은 경우라면, odd ratio를 통해 근사가 가능.
[0,1]인 probability를 $[0, \infty]$의 odds로 변환 가능.
Ex
- NC의 우승 odds가 1/9 이라면 NC의 우승확률은 1/10임.
- odds가 0.1/0.9 라면 fractional odds(분수형 배당률)은 이의 reciprocal인 9로서
- 이는 1원을 베팅할 경우 이기면 9원의 수익이 기대됨을 의미
- "받는 돈"은 "걸었던 1원 + 수익 9원" = 10원.
- A국의 월드컵 우승 odds는 1/250이라고 하면 우승확률은 1/251 (~0.398%)임.
같이보면 좋은 자료
2024.04.17 - [.../Math] - [Math] Probability 란: Probability, Odds, Likelihood
[Math] Probability 란: Probability, Odds, Likelihood
Probability란 ? 어떠한 event(사건, 사상)의 공간(=sample space, 발생가능한 모든 sample points로 구성된 set)에서특정 event(or sample point의 set으로 sample space의 subset)가 선택될(발생할) 수 있는불확실성(uncertain
dsaint31.tistory.com
'... > Math' 카테고리의 다른 글
| [Math] 수(Number)의 종류 (0) | 2022.08.31 |
|---|---|
| [Math] Radian (Circular measure, 호도법) (0) | 2022.08.29 |
| [ML] Likelihood (우도, 기대값) (0) | 2022.06.02 |
| [Math] Normal Equation : Vector derivative(Numerator Layout)를 이용한 유도 (0) | 2022.06.01 |
| [Math] 필요조건, 충분조건, 필요충분조건 (0) | 2022.05.19 |