어떤 물체가 내부에 존재하는 축(internal axis)에 대해 돌고 있는 경우, 해당 물체는 원운동(circular motion) 또는 회전(rotation)하고 있다고 말함.
Circular motion은 다음의 두가지 속력(speed)을 가짐.
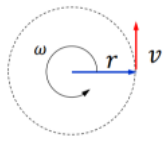
Tangential (or Linear) speed (접속 속력)
- $v$ ($m/s$)
Rotational (or Circular) speed (회전 속력, 각속력)
- $\omega$ ($\text{radian}/s$)
공학 분야에서 각(angle)에 대해 다룰 때에는 보통 radian을 사용하며 radian은 다음과 같이 정의됨.

$$\theta = \frac{s}{r}$$
- $\theta$ : angle (radian)
- $s$ : length of arc. (호의 길이)
- $r$ : radius (반지름)
사실, radian은 $s$의 길이에서 $r$의 길이를 나눈 값으로 무차원임.
여기에서 다음과 같이 tangential speed와 rotational speed가 구해짐.
$$\begin{aligned}s &= r \theta \\ \omega&=\frac{\theta}{t} \\ v &=\frac{s}{t} = \frac{r\theta}{t} = r \frac{\theta}{t} \\ &=r \omega \end{aligned}$$
회전목마나 turntable등과 같이 회전하고 있는 rigid한 물체의 경우, 회전중심에서 멀어지는, 즉 $r$이 커지는 지점일수록 tangential speed가 커지는 것과 달리 rotational speed(각속)는 모든 지점에서 동일함.
구심가속도 (centripetal acceleration or normal acceleration)
가속도는 속도의 변화율에 해당하며 등속원운동에서의 구심가속도는 다음과 같이 유도됨.

radian의 정의에 의해 구심가속도를 매우 간단하게 구한 방식이다. 등속원운동의 궤도를 삼각함수로 표현하여 구할 수도 있지만 이 방법이 훨씬 쉽다 (단, 구심가속도의 방향을 속도벡터와 직교 등은 보이지 못하는데 이는 속도의 크기로 바꾸어 처리를 해서 크기만 구할 수 있음).
angular speed 인 $\omega=\frac{v}{r}$를 대입하면 $a_c=\omega^2r$이 된다.
각가속도$\alpha=\frac{d\omega}{dt}$의 관점에서 구심가속도를 표현하면 다음과 같음.
$$a_c=\frac{d\vec{v}}{dt}=\frac{rd\omega}{dt}=r\alpha$$
'... > Physics' 카테고리의 다른 글
| Lever : 인체지레 (0) | 2022.05.09 |
|---|---|
| [Physics] Moment (모멘트) (0) | 2022.05.09 |
| [Physics] Moment of Force (or Torque) (0) | 2022.05.09 |
| [Physics] A periodic representation of wave : sin and cos (0) | 2022.04.19 |
| Mechanical Energy (0) | 2022.04.19 |