domain의 convex set인 function $f:\mathbb{R}^n\to\mathbb{R}$가 convex function임을 보이기 위한 조건.
Theorem
Vector space $\mathbb{R}^n$에서 정의된 function $f:\mathbb{R}^n\to\mathbb{R}$가 differentiable 일 경우, 다음 두 조건이 necessary and sufficient condition임.
- function $f$는 convex function임.
- domain $\text{dom }f$는 convex set이고, 임의의 $\textbf{x}_1, \textbf{x}_2 \in \text{dom }f$에 대해 다음이 성립.
$$f(\textbf{x}_1) \ge f(\textbf{x}_2) + \nabla f(\textbf{x}_2)^T(\textbf{x}_1-\textbf{x}_2)$$
증명
1이 성립할 경우, 항상 2가 성립하는지에 대한 증명 : $1\rightarrow 2$.
$q(\alpha)=f(\textbf{x}_2+\alpha(\textbf{x}_1-\textbf{x}_2))$라면 다음이 성립함.
$$\lim_{\alpha \to 0}\dfrac{ f(\textbf{x}_2+\alpha (\textbf{x}_1-\textbf{x}_2)) -f(\textbf{x}_2)}{\alpha}=\lim_{\alpha\to 0}\frac{q(\alpha)-q(0)}{\alpha}=q^\prime(0)$$
chain rule에 의해 $q^\prime(\alpha)=\nabla f(\textbf{x}_2 +\alpha(\textbf{x}_1-\textbf{x}_2))^T(\textbf{x}_1-\textbf{x}_2)$이 성립하므로, $g^\prime(0)=\nabla f(\textbf{x}_2)^T(\textbf{x}_1-\textbf{x}_2)$ 임.
$f(\textbf{x}_2 + \alpha (\textbf{x}_1-\textbf{x}_2))$는 다음이 성립함.
$$f(\textbf{x}_2 +\alpha (\textbf{x}_1 - \textbf{x}_2)) = f(\alpha \textbf{x_1} + (1-\alpha)\textbf{x}_2)$$
$f$가 convex function일 경우 다음이 성립.
$$f(\alpha \textbf{x}_1 +(1-\alpha)\textbf{x}_2) \le \alpha f(\textbf{x}_1) + (1-\alpha) f(\textbf{x}_2)$$
위의 식은 다음이 성립함.
$$\begin{aligned}f(\alpha \textbf{x}_1 +(1-\alpha)\textbf{x}_2) &\le \alpha f(\textbf{x}_1) + (1-\alpha) f(\textbf{x}_2)\\ \frac{f(\alpha \textbf{x}_1 +(1-\alpha)\textbf{x}_2)}{\alpha} &\le f(\textbf{x}_1) + \frac{1}{\alpha}f(\textbf{x}_2) - f(\textbf{x}_2)\\ \frac{f(\alpha \textbf{x}_1 +(1-\alpha)\textbf{x}_2) - f(\textbf{x}_2)}{\alpha} &\le f(\textbf{x}_1)- f(\textbf{x}_2) \\ f(\textbf{x}_2) +\frac{f(\alpha \textbf{x}_1 +(1-\alpha)\textbf{x}_2) - f(\textbf{x}_2)}{\alpha} &\le f(\textbf{x}_1)\\ f(\textbf{x}_1) &\ge f(\textbf{x}_2) +\frac{f(\textbf{x}_2+\alpha(\textbf{x}_1-\textbf{x}_2)) - f(\textbf{x}_2)}{\alpha} \end{aligned}$$
여기에 $\displaystyle \lim_{\alpha \to 0}$를 양 side에 취하면,
$$\begin{aligned} \lim_{\alpha \to 0} f(\textbf{x}_1) &\ge \lim_{\alpha \to 0}f(\textbf{x}_2) +\lim_{\alpha \to 0}\frac{f(\textbf{x}_2+\alpha(\textbf{x}_1-\textbf{x}_2)) - f(\textbf{x}_2)}{\alpha} \\ f(\textbf{x}_1) &\ge f(\textbf{x}_2)+\lim_{\alpha \to 0}\frac{f(\textbf{x}_2+\alpha(\textbf{x}_1-\textbf{x}_2)) - f(\textbf{x}_2)}{\alpha} \\ f(\textbf{x}_1) &\ge f(\textbf{x}_2)+\lim_{\alpha \to 0}\frac{f(\textbf{x}_2+\alpha(\textbf{x}_1-\textbf{x}_2)) - f(\textbf{x}_2)}{\alpha (\textbf{x}_1-\textbf{x}_2)}(\textbf{x}_1-\textbf{x}_2) \\ f(\textbf{x}_1) &\ge f(\textbf{x}_2) + \nabla f(\textbf{x}_2)^T(\textbf{x}_1-\textbf{x}_2)\end{aligned}$$
2가 성립할 경우, 항상 1이 성립하는지에 대한 증명 : $1\leftarrow 2$.
모든 $\textbf{x}_1, \textbf{x}_2 \in \text{dom }f$에 대해 $f(\textbf{x}_1) \ge f(\textbf{x}_2) + \nabla f(\textbf{x}_2)^T(\textbf{x}_1-\textbf{x}_2)$ 가 성립하면서, $[0,1]$에 속하는 real number $\alpha$에 대해 $\textbf{x}_3 = \alpha \textbf{x}_1+(1-\alpha)\textbf{x}_2$라고 정의하면, convex set의 정의에 의해 $\textbf{x}_3 \in \text{dom }f$이며, 다음이 성립함.
$$f(\textbf{x}_1) \ge f(\textbf{x}_3) +\nabla f(\textbf{x}_3)^T (\textbf{x}_1-\textbf{x}_3) \\ f(\textbf{x}_2) \ge f(\textbf{x}_3) +\nabla f(\textbf{x}_3)^T (\textbf{x}_2-\textbf{x}_3)$$
위의 식에 $\alpha$와 $1-\alpha$를 곱하고 이 두 식을 더해주면 다음이 성립함.
$$\begin{aligned} \alpha f(\textbf{x}_1) + (1-\alpha) f (\textbf{x}_2) \ge &\alpha f(\textbf{x}_3) + \alpha \nabla f(\textbf{x}_3)^T (\textbf{x}_1-\textbf{x}_3) \\ &+ (1-\alpha)f(\textbf{x}_3) + (1-\alpha)\nabla f(\textbf{x}_3)^T (\textbf{x}_2-\textbf{x}_3) \\ \end{aligned}$$
위의 식의 right side는 다음과 같음.
$$\begin{aligned} \alpha f(\textbf{x}_3) + \alpha \nabla f(\textbf{x}_3)^T (\textbf{x}_1-\textbf{x}_3) + (1-\alpha)f(\textbf{x}_3) + (1-\alpha)\nabla f(\textbf{x}_3)^T (\textbf{x}_2-\textbf{x}_3) &= (\alpha +1 -\alpha)f(\textbf{x}_3) + \nabla f(\textbf{x}_3)^T (\alpha(\textbf{x}_1-\textbf{x}_3)+(1-\alpha)(\textbf{x}_2-\textbf{x}_3)) \\ &=f(\textbf{x}_3) +\nabla f(\textbf{x}_3)^T (\alpha \textbf{x}_1 +(1-\alpha) \textbf{x}_2 - \textbf{x}_3) \\ &= f(\textbf{x}_3) \\ &= f(\alpha \textbf{x}_1 +(1-\alpha) \textbf{x}_2) \end{aligned}$$
즉, 다음이 성립함.
$$\alpha f(\textbf{x}_1) + (1-\alpha) f (\textbf{x}_1) \ge f(\alpha \textbf{x}_1 +(1-\alpha) \textbf{x}_2)$$
위의 식은 $f$가 convex function임을 의미한다. 즉, sufficient condition이 성립.
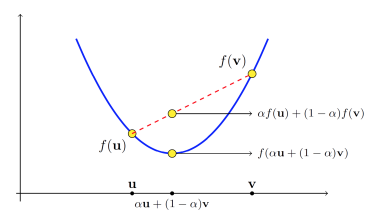
비슷한 Theorem (Jensen's inequality)으로, 임의의 $\textbf{x}_1, \textbf{x}_2 \in \text{dom }f$이고 $[0,1]$인 $\alpha$에 대해 다음의 부등식이 성립한다.
$$ f(\alpha\textbf{x}_1+(1-\alpha)\textbf{x}_2) \le \alpha f(\textbf{x}_1) + (1-\alpha)f (\textbf{x}_2)$$
- left side는 $\textbf{x}_1,\textbf{x}_2$사이에 존재하는 $\alpha\textbf{x}_1+(1-\alpha)\textbf{x}_2$에서의 실제 convex function $f$의 함수값.
- right side는 $\alpha\textbf{x}_1+(1-\alpha)\textbf{x}_2$의 함수값을 $\textbf{x}_1,\textbf{x}_2$에서의 함수값들을 bilinear interpolation을 하여 구한 것임
- convex이므로 bilinear interpolation한 값이 항상 커야함.
'... > Math' 카테고리의 다른 글
| [Math] Stationary point (or Critical point) (0) | 2023.07.10 |
|---|---|
| [Math] Second Order Condition : Convexity (0) | 2023.07.10 |
| [Math] Linear Programming and Quadratic Programming (0) | 2023.07.08 |
| [Math] A regular point of the feasible set. (0) | 2023.07.07 |
| [Math] Duality (쌍대성) 이란 : Optimization에서 (0) | 2023.07.07 |