[Math] Level Set

real multi-variate function $f:\mathbb{R}^n \to \mathbb{R}$ 에서 Level Set은 real value $c$에 대해 다음을 만족하는 set을 의미함.

 

$$\left\{ (x_1, \dots, x_n) \in \mathbb{R}^n | f(x_1, \dots, x_n)=c \right\}$$

 

위의 정의를 따르면서

• $n=2$인 경우의 Level Set을 Level curve (등위곡선)라고 부르며,
• $n=3$인 경우의 Level Set을 Level surface (등위곡면)라고 부름.

지도에서 등고선이 Level curve의 예라고 할 수 있다. x,y좌표에서 높이를 z라고 하면 일종의 $n=2$인 multi-variate function이라고 할 수 있다. 

$$z=f(x,y)$$

• 이 때, 등고선이 바로 Level curve임.

ori. : https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=ksjin0212&logNo=221467395079

 

 

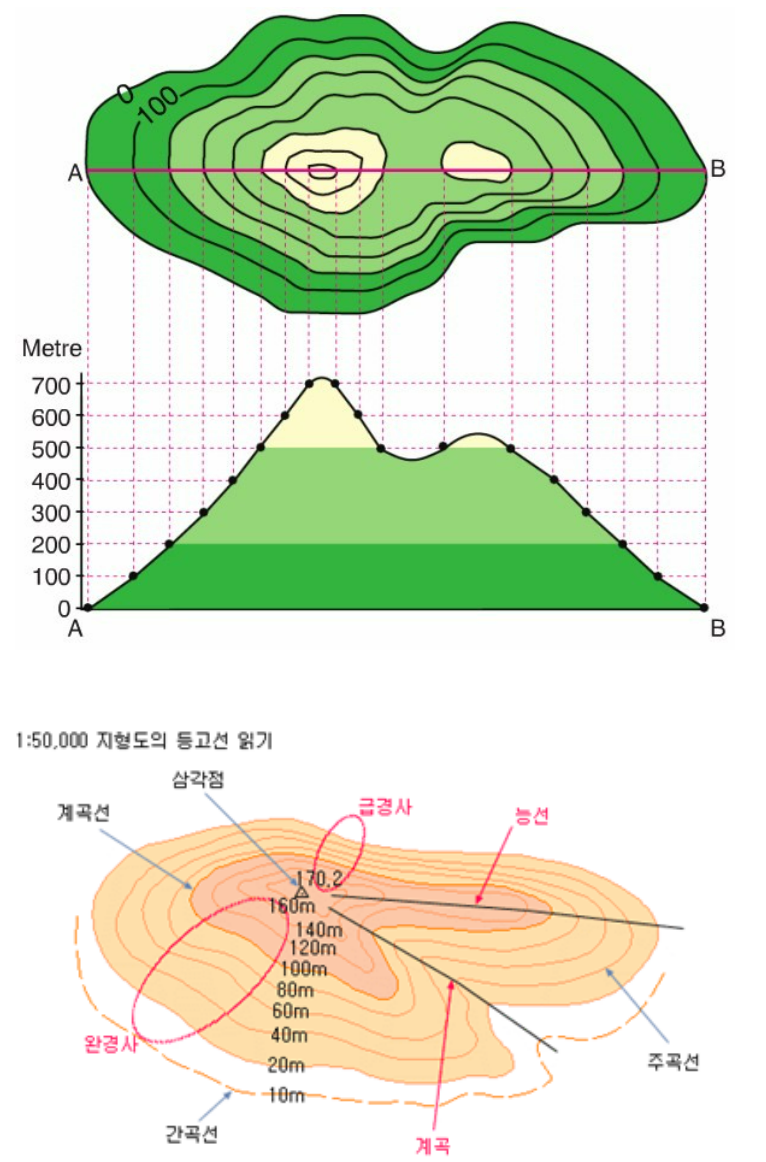
보다 자세한 건 다음 URL을 참고
https://mathworld.wolfram.com/LevelSet.html