명칭의 유래
- LASSO: Least Absolute Shrinkage and Selection Operator 의 약자
- 이름에서 알 수 있듯이,
- 절대값(absolute value) 기반의
- shrinkage(축소)와
- feature selection(특성 선택)을 동시에 수행하는 회귀 기법
- “Shrinkage”는 weight의 크기를 줄이는 정칙화 효과, “Selection”은 일부 weight를 정확히 0으로 만들어 feature를 제거하는 효과를 의미함
역사
- Tibshirani (1996) 에 의해 제안됨
- Ridge Regression이 모든 weight를 균일하게 줄이는 것과 달리,
Lasso는 일부 weight를 0으로 만들어 희소성(sparsity) 을 유도 - 주로 convex optimization 에서 자주 사용됨.
- L1 norm을 사용한 penalty term을 포함하는 Lasso는 Tikhonov regularization의 변형으로 볼 수 있으나, penalty 함수의 형태가 절댓값으로 바뀐 점이 결정적 차이점을 가짐.
참고: L1 vs L2 정칙화의 특성
| 구분 | L1 정칙화 (Lasso) | L2 정칙화 (Ridge) |
| Penalty | $\lambda \sum w_j $ | $\lambda \sum w_j^2$ |
| 결과 | Sparse solution (일부 0) | Smooth shrinkage (모두 작아짐) |
| Feature selection | 가능 | 불가능 |
| 해석 용이성 | 높음 | 낮음 |
| 안정성 | 낮음 (상관특성 간 불안정) | 높음 (multicollinearity 완화) |
Lasso Regression (L1 정규화)
Objective Function
$$L = \displaystyle \frac{1}{m}\sum_{i=1}^{m} (y_i - \hat{y}_i)^2 + \lambda \sum_{j=1}^{n} |w_j|$$
- $m$ : sample 수
- $n$ : feature 수
- $\lambda$ : regularization 강도 (hyperparameter)
Gradient (subgradient)
$$\frac{\partial L}{\partial w_j} = -\frac{2}{m}\sum_{i=1}^{m}(y_i - \hat{y}_i)x_{ij} + \lambda \cdot \text{sign}(w_j)$$
단, $w_j = 0$ 인 구간에서는 미분 불가능하므로 subgradient 사용.
2025.11.02 - [Programming/ML] - Subgradient 와 Gradient Descent
Subgradient 와 Gradient Descent
Prerequistes모델 학습의 목표는손실 함수 $L(\boldsymbol{\omega}, \textbf{X})$를 최소화하는파라미터 $\boldsymbol{\omega}$를 찾는 것임.이때 가장 기본적인 최적화 방법은 Gradient Descent(경사 하강법)임:$$\boxed{\bo
dsaint31.tistory.com
특징
- 일부 $w_j$가 정확히 0이 되어 불필요한 특성을 제거
- 모델 단순화 및 해석 용이성 증가
- 그러나 feature 간 강한 상관(multicollinearity)이 존재할 때, feature selection이 불안정해질 수 있음
Ridge Regression (L2 정규화)와의 비교
- Ridge: 모든 weight를 작게 만드는 연속적 축소(continuous shrinkage)
- Lasso: 일부 weight를 완전히 제거(sparse selection)
- 실제 모델링에서는 두 기법을 혼합한 Elastic Net이 자주 사용됨
$$
L = \frac{1}{m}\sum (y_i - \hat{y}_i)^2 + \lambda_1 \sum |w_j| + \lambda_2 \sum w_j^2
$$
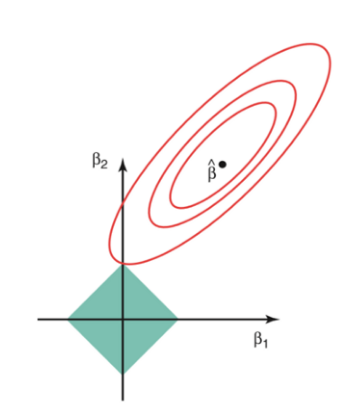
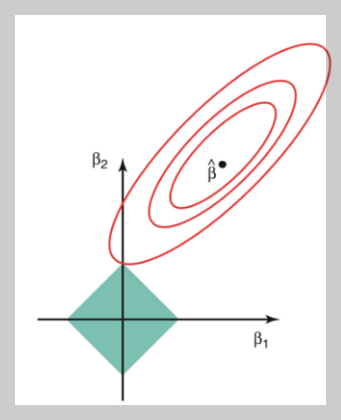
기하학적 해석
- L2 제약(Ridge): 원형(circle) => 모든 방향 동일한 제약
- L1 제약(Lasso): 마름모(diamond) 형태
- Loss function의 contour와 마름모의 꼭짓점이 만나는 지점에서 해가 발생
- 꼭짓점에서 일부 ( $w_j = 0$ )이 되어 sparse solution 유도
- 이 차이로 인해, Ridge는 “모두 조금씩 줄이지만 0은 만들지 않음”, Lasso는 “일부를 완전히 0으로” 만드는 효과를 가짐

기타
Ridge 의 경우처럼, Regularization Term을 샘플 수로 나누는 처리가 보통 이루어지며, bias에 대해선 규제를 하지 않기도 함.
2025.11.06 - [Programming/ML] - Ridge Regression
Ridge Regression
명칭의 유래Ridge: "산등성이" 또는 "융기"를 의미하는 영어 단어L2-Regularization Term 추가 시 loss function의 contour가 융기된 형태로 변형되는 데에서 유래됨.역사적 배경Tikhonov regularization (1963)과 수학
dsaint31.tistory.com
요약
- Lasso Regression은 L1 정칙화 기반 회귀모델
- 일부 weight를 0으로 만들어 feature selection 효과 제공
- Ridge에 비해 해석 용이하지만, 안정성은 다소 떨어짐
- 데이터 규모와 상관없는 일관된 (\lambda)를 위해 평균화 필요
- bias는 규제하지 않음 (평행이동 불변성 유지)
- Ridge와 Lasso의 중간형으로 Elastic Net이 실무에서 자주 사용됨
같이보면 좋은 자료들
2024.10.27 - [Programming/ML] - [ML] Regularization
[ML] Regularization
Regularization 이란?기계 학습과 딥러닝에서 Regularization은 모델이 overfitting(과적합)되지 않도록 도와주는 기법을 의미함.Overfitting(과적합)은 모델이 훈련 데이터에 너무 잘 맞아 새로운 데이터에 대
dsaint31.tistory.com
[ML] Classic Regressor (Summary) - regression
DeepLearning 계열을 제외한 Regressor 모델들을 간단하게 정리함.https://gist.github.com/dsaint31x/1c9c4a27e1d841098a9fee345363fa59 ML_Regressor_Summary.ipynbML_Regressor_Summary.ipynb. GitHub Gist: instantly share code, notes, and snippets.g
ds31x.tistory.com
2025.11.06 - [Programming/ML] - Ridge Regression
Ridge Regression
명칭의 유래Ridge: "산등성이" 또는 "융기"를 의미하는 영어 단어L2-Regularization Term 추가 시 loss function의 contour가 융기된 형태로 변형되는 데에서 유래됨.역사적 배경Tikhonov regularization (1963)과 수학
dsaint31.tistory.com
2025.11.02 - [Programming/ML] - Subgradient 와 Gradient Descent
Subgradient 와 Gradient Descent
Prerequistes모델 학습의 목표는손실 함수 $L(\boldsymbol{\omega}, \textbf{X})$를 최소화하는파라미터 $\boldsymbol{\omega}$를 찾는 것임.이때 가장 기본적인 최적화 방법은 Gradient Descent(경사 하강법)임:$$\boxed{\bo
dsaint31.tistory.com
'Programming > ML' 카테고리의 다른 글
| ULMFit : Transfer Learning for NLP (0) | 2026.01.16 |
|---|---|
| Overfitting (과적합) (0) | 2025.11.20 |
| Ridge Regression (1) | 2025.11.06 |
| Subgradient 와 Gradient Descent (0) | 2025.11.02 |
| Bias-Variance Tradeoff (0) | 2025.10.30 |